 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Комплексные числа в тригонометрической форме
Комплексное число 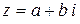 изображается в виде вектора
изображается в виде вектора 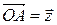 с началом в точке
с началом в точке 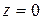 и концом в точке
и концом в точке 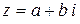 . Угол
. Угол 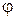 между действительной осью Ох и вектором
между действительной осью Ох и вектором 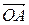 , отсчитываемый от положительного направления действительной оси, называется аргументом комплексного числа
, отсчитываемый от положительного направления действительной оси, называется аргументом комплексного числа  (рис. 10.4).
(рис. 10.4).
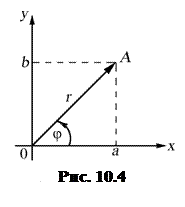 Если отсчет ведется против часовой стрелки, то величина угла считается положительной, если по движению часовой стрелки – отрицательной. Аргумент
Если отсчет ведется против часовой стрелки, то величина угла считается положительной, если по движению часовой стрелки – отрицательной. Аргумент 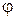 комплексного числа
комплексного числа 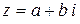 записывается так:
записывается так: 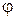 =
= 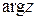 или
или 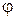 =
=  (
( ).
).
Аргумент комплексного числа определяется неоднозначно. Любое комплексное число  имеет бесконечное множество аргументов, отличающихся друг от друга на число, кратное 2
имеет бесконечное множество аргументов, отличающихся друг от друга на число, кратное 2 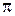 . Аргумент комплексного числа определяется однозначно, если область его изменения ограничить промежутком величины 2
. Аргумент комплексного числа определяется однозначно, если область его изменения ограничить промежутком величины 2 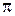 . В качестве такого промежутка принято брать один из следующих промежутков
. В качестве такого промежутка принято брать один из следующих промежутков 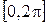 ,
, 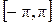 . Такое значение аргумента
. Такое значение аргумента 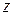 называется главным значением аргумента
называется главным значением аргумента  . Так как аргумент
. Так как аргумент 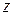 определяется с точностью до слагаемого
определяется с точностью до слагаемого 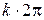 , то
, то
 . (10.7)
. (10.7)
Из рисунка видно, что
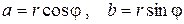 , (10.8)
, (10.8)
 ,
,  .
.
Запишем формулы для вычисления главного значения аргумента, принадлежащие промежутку 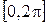 :
:
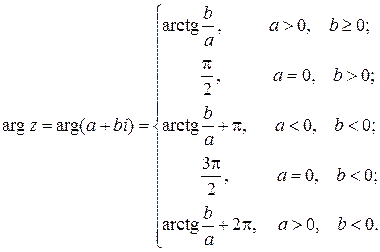 (10.9)
(10.9)
Для представления комплексного числа 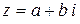 в тригонометрической форме необходимо найти:
в тригонометрической форме необходимо найти:
1) модуль этого числа  ; изобразить точку
; изобразить точку  и выбрать нужное значение аргумента этого числа;
и выбрать нужное значение аргумента этого числа;
1) записать 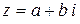 , воспользовавшись соотношением (2.8). Получаем тригонометрическую форму комплексного числа
, воспользовавшись соотношением (2.8). Получаем тригонометрическую форму комплексного числа
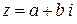 =
= 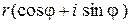 . (10.10)
. (10.10)
10.1.3. Действия над комплексными числами
в тригонометрической форме
При умножении двух или нескольких чисел их модули перемножаются, а аргументы складываются:
 (10.11)
(10.11)
При делении двух комплексных чисел модуль числителя делится на модуль знаменателя, а аргумент знаменателя вычитается из аргумента числителя:
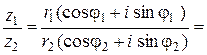
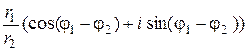 . (10.12)
. (10.12)
При возведении комплексного числа в целую положительную степень модуль его возводится в ту же степень, а аргумент умножается на показатель степени, т. е.

 , (10.13)
, (10.13)
где  . Эта формула называется формулой Муавра.
. Эта формула называется формулой Муавра.
Корень 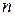 -й степени из комплексного числа
-й степени из комплексного числа 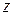 =
= 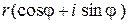 имеет
имеет 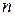 различных значений, которые находятся по формуле
различных значений, которые находятся по формуле
 , (10.14)
, (10.14)
где 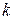 = 0, 1, 2,…,
= 0, 1, 2,…, 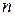 –1.
–1.
Пример 8.Записать комплексное число  в тригонометрической форме.
в тригонометрической форме.
Решение.Чтобы записать комплексное число в тригонометрической форме нужно знать его модуль и аргумент, по формуле (10.5) находим
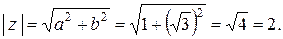
Затем подсчитываем главное значение аргумента 
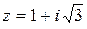 . Вещественная и мнимая части данного комплексного числа положительны (
. Вещественная и мнимая части данного комплексного числа положительны (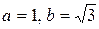 ). По формуле (10.9) главное значение аргумента совпадает с
). По формуле (10.9) главное значение аргумента совпадает с 
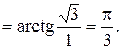
Тогда  .
.
Ответ:  .
.
Пример 9. Записать в тригонометрической форме комплексное число 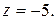
Решение. Данное число является вещественным и отрицательным, а главное значение его аргумента (см. формулу (10.9)) равно 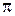 . Подсчитаем модуль числа
. Подсчитаем модуль числа
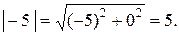
Модуль и аргумент числа –5 найдены, по формулам (10.7) – (10.9) имеем 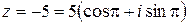 .
.
Ответ: 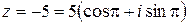 .
.
Пример 10. Найти аргумент числа 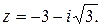
Решение.Вещественные и мнимые части данного числа отрицательны и по формуле (2.9) главное значение аргумента его совпадает с
 .
.
Следовательно, 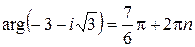 .
.
Пример 11.Найти произведение чисел  , где
, где
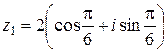 ,
, 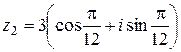 .
.
Решение.  =
=  =
= 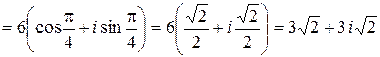 .
.
Ответ: 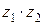 =
= 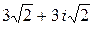 .
.
Пример 12. Найти произведение чисел  , где
, где
 ,
,  .
.
Решение.
 =
= 
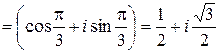 .
.
Ответ:  =
= 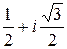 .
.
Пример 13.Найти частное чисел  и
и 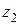 , где
, где
 ,
,  .
.
Решение.
 =
=  =
=
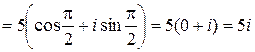 .
.
Ответ:  =
= 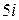 .
.
Пример 14.Найти  , где
, где  .
.
Решение.Возводим в шестую степень 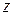 , согласно формуле (10.13):
, согласно формуле (10.13):
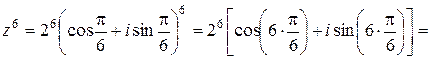
= 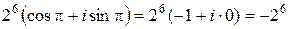 .
.
Ответ:  =
= 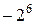 .
.
Пример 15. Найти 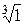 .
.
Решение.Поскольку 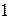 =
= 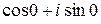 , то
, то 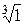 состоит из чисел
состоит из чисел
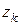 =
= 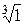 =
= 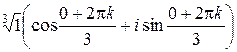 ,
,
где 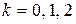 (см. формулу (10.14)).
(см. формулу (10.14)).
Задаем k = 0, получим 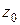 =
= 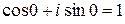 ;
;
k = 1, получим 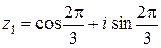 =
=  ;
;
k = 2, получим 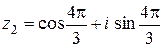 =
= 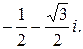
Ответ: 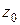 =
= 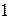 ;
; 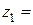 =
=  ;
; 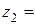
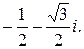
Пример 16. Найти 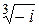 .
.
Решение. Поскольку  =
= 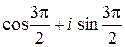 , то
, то  состоит из чисел
состоит из чисел
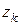 =
= 
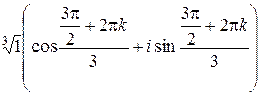 .
.
Задаем 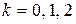 . Получаем
. Получаем 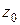 =
= 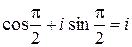 ,
,
 =
= 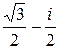 ,
,
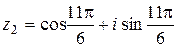 =
= 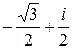 .
.
Ответ: 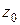
 ,
,  =
= 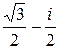 ,
, 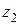 =
= 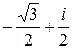 .
.
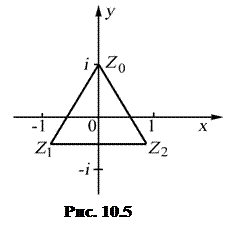 Отметим, что точки плоскости
Отметим, что точки плоскости 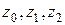 (рис. 2.5) являются вершинами правильного треугольника. Это не случайно – для любого
(рис. 2.5) являются вершинами правильного треугольника. Это не случайно – для любого  и любого
и любого 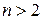 корни степени n из числа
корни степени n из числа 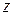 являются вершинами правильного
являются вершинами правильного 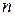 -угольника с центром в нуле (рис. 2.5).
-угольника с центром в нуле (рис. 2.5).
 2.2. Задачи более сложного типа
2.2. Задачи более сложного типа
Пример 17. Составить квадратное уравнение с действительными коэффициентами, если известен один из его корней 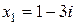 .
.
Решение.Если  – корень уравнения с действительными коэффициентами, то и
– корень уравнения с действительными коэффициентами, то и 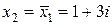 – тоже корень этого уравнения. Тогда левая часть квадратного уравнения раскладывается на множители
– тоже корень этого уравнения. Тогда левая часть квадратного уравнения раскладывается на множители
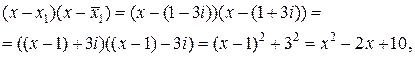
т. е. искомое квадратное уравнение имеет вид 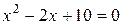 . Этот же результат можно получить, производя решение по формуле Виета.
. Этот же результат можно получить, производя решение по формуле Виета.
Ответ: 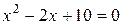 .
.
Пример 18.Решить уравнение  .
.
Решение.Так как два комплексных числа  и
и  называются равными, если
называются равными, если  и
и 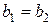 , то преобразуем наше уравнение к виду
, то преобразуем наше уравнение к виду
 ,
,
тогда решая уравнения
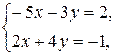
получаем

Ответ: 
 Пример 19. Изобразить множества точек, для которых выполняются заданные условия:
Пример 19. Изобразить множества точек, для которых выполняются заданные условия: 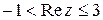 .
.
Решение. Поскольку 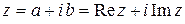 , имеем
, имеем  . Действительные числа
. Действительные числа 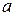 изображаются точками оси абсцисс (рис. 2.6), значит, мы имеем область – вертикальную полосу, ограниченную прямыми:
изображаются точками оси абсцисс (рис. 2.6), значит, мы имеем область – вертикальную полосу, ограниченную прямыми: 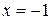 и
и 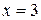 (точки прямой
(точки прямой 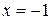 в область не входят, поэтому эта прямая изображена пунктиром).
в область не входят, поэтому эта прямая изображена пунктиром).
Пример 20.Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству
 .
.
Решение. Поскольку  , имеем
, имеем

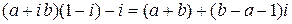 .
.
Найдем модуль полученного комплексного числа
| 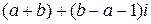 |=
|= 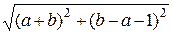
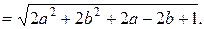
По условию
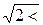
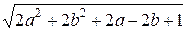
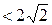 , или
, или
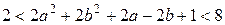 ,
,
 .
.
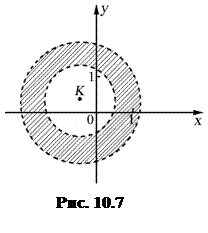 Выделяя полные квадраты по
Выделяя полные квадраты по 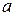 и
и  , получим
, получим
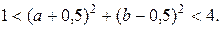
Это неравенство представляет собой внутренность кольца (рис. 2.7), т. к. левая часть двойного неравенства – область, лежащая вне круга радиусом 1с центром в точке С (–0,5; 0,5), правая часть – круг с центром в точке С и радиусом, равным 2 (границы окружностей в область не входят, поэтому они изображены пунктиром).
Пример 21. Найти наибольшее и наименьшее значения 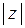 , если
, если 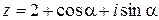 .
.
Решение.Имеем
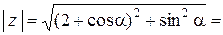
= 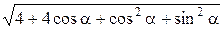 =
=  .
.
Анализируя полученное 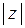 =
=  , делаем вывод, что наибольшее значение
, делаем вывод, что наибольшее значение 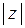 равно
равно 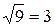 (при
(при 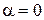 ), а наименьшее значение
), а наименьшее значение 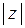 равно
равно 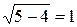 (при
(при 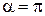 ).
).
Ответ: наибольшее значение 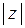 = 3 (при
= 3 (при 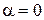 ), а наименьшее значение
), а наименьшее значение 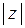 = 1 (при
= 1 (при 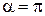 ).
).
Пример 22.Решить неравенство
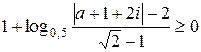 . (*)
. (*)
Решение.ОДЗ: 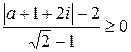 , отсюда
, отсюда  ; находя модуль, имеем
; находя модуль, имеем  или
или 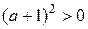 , тогда
, тогда  .
.
Из (*) имеем  , по определению
, по определению  . Из последнего неравенства имеем
. Из последнего неравенства имеем  , преобразовывая, получаем
, преобразовывая, получаем 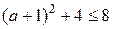 , т. е.
, т. е. 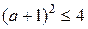 или
или  , окончательно
, окончательно 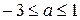 .
.
При условии 
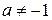 получаем, что неравенству (*) удовлетворяет множество [–3;1)
получаем, что неравенству (*) удовлетворяет множество [–3;1) 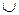 (–1;1].
(–1;1].
Ответ: [–3;1) 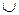 (–1;1].
(–1;1].
Вопросы и задания для самоподготовки
1. Какое число называется мнимой единицей?
2. Назвать комплексные числа в алгебраической форме?
3. Перечислить действия над комплексными числами в алгебраической форме.
4. Назвать геометрический образ комплексного числа?
5. Назвать комплексные числа в тригонометрической форме?
6. Какое значение аргумента называется главным?
7. Назвать действия над комплексными числами, заданными в тригонометрической форме?
8. Записать формулу, по которой осуществляется возведение комплексного числа в целую положительную степень.
9. Записать формулу, по которой находится корень 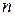 -й степени из комплексного числа.
-й степени из комплексного числа.
10. Вершинами чего являются корни степени 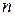 из числа
из числа 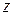 ?
?
Поиск по сайту: