 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Абсолютная величина числа
Литература.
1. Математика для экономистов: учебное пособие / С.И. Макаров. – М.: КНОРУС, 2008.
2. Высшая математика для экономистов: учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман. – М.: ЮНИТИ, 2001.
3.Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике: учебник: в 2-х ч.. – М.: Финансы и статистика, 2003.
4. Математика для экономистов. Задачник:учебно-практическое пособие / кол. авторов; под ред. С.И. Макарова, М.В. Мищенко. – М.: КНОРУС, 2008.
Лекция 1.
Математическая символика
Логические символы
- для любого, любой
- существует
: - такой, что
- и
- или
- следует
- тогда и только тогда (необходимо и достаточно)
┐- символ отрицания
Теоретико-множественные символы
-объединение
-пересечение
- разность 
С – дополнение
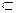- включается, входит
- принадлежит
- пустое множество
Элементы теории множеств
Множество – совокупность элементов, объединенных по какому-либо признаку.
А={ 
}
Пусть А, В, С – некоторые множества. Тогда над ними можно совершать следующие операции:
1. Объединение множеств:
.
2. Пересечение множеств:
.
3. Разность множеств:
.
4. Дополнение множества в другом множестве:
.
Самостоятельно: свойства операций над множествами.
Стандартные множества
N = {1, 2, 3, …} – натуральные числа
Z = { N, N 
, 0} – целые числа
P = {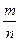 
, где 
Z, 
N, - взаимно простые} – рациональные числа
(конечные или периодические десятичные дроби)
Q – иррациональные числа (бесконечные непериодические десятичные
дроби)
R = { P Q } – действительные числа.
Элементы множества R называются собственными точками;
- несобственные точки.
Виды промежутков:
-отрезок
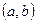- интервал
, 
- полуинтервал.
Абсолютная величина числа
Опр. Абсолютной величиной (модулем) действительного числа х называется само число х, если оно неотрицательно и противоположное ему число – х, если оно отрицательно:
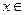R,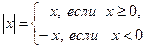 
Свойства модуля:
1. 
2. 
3. 
4. 
5. 
6. 
, (
).
7. Первое неравенство треугольника: 
R:
.
Второе неравенство треугольника: R:
.
Поиск по сайту: