 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Понятие о дифференциальных уравнениях
Дифференциальным уравнением называется уравнение, связывающее искомую функцию, аргумент и производные различных порядков данной функции.
Простой пример дифференциального уравнения дает задача о нахождении первообразной F(x) для заданной функции f(x), т.к. ее вполне можно рассматривать как задачу о нахождении функции F(x), удовлетворяющей уравнению F'(x)=f(x).
В общем случае дифференциальное уравнение можно записать в виде
,
где G — некоторая функция, при этом порядок n старшей производной, входящей в запись уравнения, называется порядком дифференциального уравнения. Например, задача о нахождении первообразной приводит к дифференциальному уравнению первого порядка, уравнение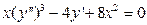 
- второго порядка и т.п.
Дифференциальное уравнение называется разрешенным относительно старшей производной, если оно имеет вид
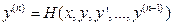
где Н— некоторая функция.
Решением (или интегралом) дифференциального уравнения называется такая функция у=f(х), которая при подстановке ее в это уравнение обращает его в тождество. Например, функция y=sin x является решением уравнения у «+у=0, так как (sin x)»+ sin x=0 для любых x.
Задача о нахождении решения дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.
Отметим, что без дополнительных предположений решение дифференциального уравнения принципиально неоднозначно, т.е., аналогично неопределенному интегралу, содержит постоянные константы Сi, число которых равно порядку уравнения. Такое решение называется общим решением дифференциального уравнения. Для определения этих постоянных и получения однозначного частногорешения используются дополнительные условия, которые задают значения решения либо в точке х=0 (начальные условия), либо в точках х¹0 (граничные условия).
В нашем курсе ограничимся изучением дифференциальных уравнений первого порядка 
(или 
) и простейших уравнений второго порядка.
Уравнения первого порядка с разделяющимися переменными
Уравнение называется дифференциальным уравнением первого порядка с разделяющимися переменными, если, после преобразований, его можно привести к виду
Такие уравнения решаются обычным интегрированием левой и правой частей. Пример:
Таким образом, уравнение свелось к вычислению обычного неопределенного интеграла. Единственным, не слишком существенным отличием, является то, что постоянная С может входить в алгебраические операции как составная часть. Полученное решение, содержащее произвольную постоянную, будет общим решением (общим интегралом) данного уравнения. Рассмотрим, как выглядят частные решения, если поставлены какие-либо дополнительные условия.
· Пусть известно значение функции в точке х=0 (начальное условие), например, у(0)=3. Подставим в общее решение:
.
· Пусть известно значение функции в точке 
(граничное условие), например, у(2)=5. Подставим в общее решение:
.
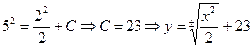Результат, в котором определено конкретное значение константы С с помощью начального или граничного условия и будет частным решением (частным интегралом) дифференциального уравнения.
Понятие о дифференциальных уравнениях второго порядка
Общая форма уравнения второго порядка 
. Ограничимся иллюстрацией случая 
, когда общее решение может быть получено последовательным интегрированием. Пример:
т.е., после первого интегрирования результатом будет первая производная. Проинтегрируем еще раз для получения общего решения
.
Произвольные постоянные 
и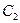 
могут быть вычислены при наличии начальных или граничных условий.
· Пусть в точке х=0 заданы начальные условия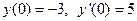 
. Подставим в полученное общее решение:
.
Таким образом, частное решение 
.
· Пусть заданы граничные условия 
. Подставим в то же общее решение:
.
Таким образом, частное решение 
.
Обратим внимание, что условия для уравнений второго порядка обладают вариабельностью: можно задавать в точке как значение функции, так и ее первой производной.
Примеры решения задач
1. Вычислить 
.
В данном случае – приводим к табличному виду 
.
2. Вычислить 
.
Здесь для приведения к табличному виду 
преобразуем подынтегральное выражение к сумме двух слагаемых:
.
3. Вычислить интеграл 
.
Здесь для применения табличной формулы 
необходимо преобразовать показатель степени (2 x – 1). Введем подстановку: u = 2 x – 1, откуда du = 2 dx и 
. Тогда:
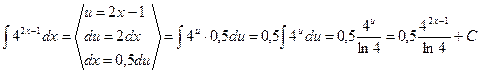
4. Вычислить интеграл 
.
5. Вычислить интеграл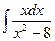 
.
6. Вычислить интеграл 
.
7. Вычислить интеграл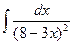 
.
8. Вычислить интеграл 
.
Так как 
, то 
9. Вычислить интеграл 
.
Приведем интеграл к табличному виду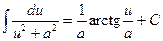 
.
10. Вычислить интеграл 
.
Интегралы такого типа вычисляются с помощью формулы интегрирования по частям 
11. Вычислить интеграл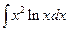 
.
12. Вычислить интеграл 
.
| 2 x – 1 | x +1 | |
| Делим: | 2 x + 2 | |
| –3 |
|
и
.
13. Вычислить интеграл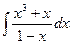 
.
| x 3 + 0 × x 2 + x +0 | – x + 1 | ||||||
| Делим: | x 3 - x 2 | – x 2 – x – 2 | |||||
| x 2 + x | |||||||
| x 2 – x | |||||||
| 2 x + 0 | |||||||
| 2 x – 2 | |||||||
|
, откуда 
14. Вычислить интеграл 
.
Так как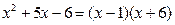 
, то 
. Приведем правую часть к общему знаменателю:
.
Отбрасывая знаменатели и открывая скобки, получим
.
Чтобы два алгебраических выражения были тождественно равны, следует обеспечить равенство соответственных коэффициентов. Получаем систему уравнений:
.
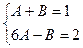Отсюда 
; 
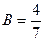и 
. Таким образом,
.
15. Вычислить интеграл 
.
Дискриминант знаменателя 
, поэтому разложить знаменатель на множители не удается. Здесь можно было бы использовать подстановку 
, но, заглянув в «Таблицы интегралов» в справочнике М.Я.Выгодского, находим формулу:
при 
.
В нашем случае 
. После подстановки и вычислений получим:
.
16. Вычислить интеграл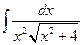 
.
В том же справочнике находим общую формулу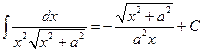 
.
В нашем примере a 2=4, следовательно 
17. Решить уравнение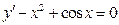 
.
Решение:
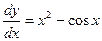Þ 
Þ 
.
Интегрируем обе части полученного выражения 
, откуда
.
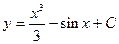Дифференцированием можно проверить правильность полученного результата.
18. Решить уравнение 
.
Решение:
Так как C – произвольная постоянная, то ее можно записать в любой удобной форме. Поэтому используем запись:
Þ 
Þ 
Þ 
Þ 
.
19. Найти частное решение уравнения 
, удовлетворяющее граничному условию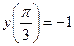 
.
Решение:
Интегрируем:
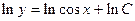Þ 
Þ 
.
По заданному граничному условию найдем значения константы C:
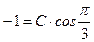или 
, т.е. C= –2.
Искомое частное решение имеет вид 
20. Найти решение уравнения 
, удовлетворяющее начальным условиям 
.
Здесь двумя последовательными интегрированиями получим общее решение:
,
.
Подставим начальные условия и получим значения констант: С1= 5, С2= 1. Следовательно, искомое частное решение имеет вид:
.
Вопросы для самоконтроля:
1. Понятие неопределенного интеграла.
2. Свойства неопределенного интервала.
3. Замена переменной в неопределенном интеграле.
4. Интегрирование по частям.
5. Интегрирование дробей делением числителя на знаменатель.
6. Метод неопределенных коэффициентов.
7. Интегрирование с помощью таблиц.
8. Понятие дифференциального уравнения.
9. Уравнения первого порядка с разделяющимися переменными.
10. Понятие об уравнениях второго порядка.
11. Начальные условия.
12. Граничные условия.
Поиск по сайту: