Общая схема исследования функции и построения графиков

В современных условиях построение графиков осуществляется на практике, как правило, по точкам или с помощью компьютера. Однако в задачах с повышенной ответственностью необходимо использовать описанные выше приемы. Полная последовательность анализа функции и построения ее графика состоит из следующих этапов:

· Находится область определения функции 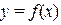и вертикальные асимптоты, если они есть.

· Устанавливается тип функции: четная, нечетная, общего вида.

· Из решения уравнения 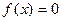определяются корни функции, т.е. точки ее пересечения с осью оХ.

· Вычисляются производные 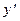и .

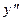· Определяются экстремумы функции.

· Определяются точки перегиба и исследуются выпуклости функции.

· Проверяется наличие горизонтальных и наклонных асимптот.

· При необходимости детализации, вычисляются значения функции в нескольких дополнительных точках.

· Все полученные результаты отображаются на плоскости, и строится график.

Расчеты и отображение результатов обычно делаются одновременно. Этапы 2, 6 и 7, во многих случаях, можно опустить.

Примеры решения задач

Наиболее часто встречающимися применениями дифференцирования на практике являются раскрытие неопределенных пределов (правило Лопиталя) и исследование особенностей изменяемости функций, в том числе построение графиков функций. Приведем типовые примеры по теме.

1. Вычислить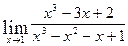

Решение: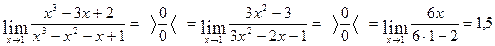

Ответ: 1,5.

2. Вычислить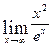

Решение: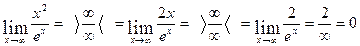

Ответ: функция – бесконечно малая при .

3. Вычислить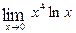

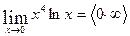. Для раскрытия неопределенности такого типа следует предварительно преобразовать произведение в дробь.

Возможны два варианта:

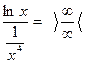или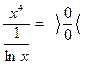

Только после этого можно применить правило Лопиталя. Используя первый вариант, получим:

.

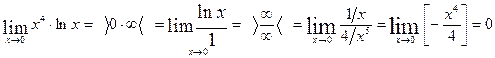Ответ: функция – бесконечно малая при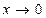

4. Вычислить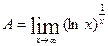

Здесь имеет место случай 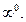Для раскрытия таких пределов удобно сначала прологарифмировать заданную функцию и затем применить правило Лопиталя. Имеем:

.

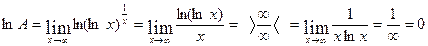Так как ln A = 0, то А = е ⁰ = 1.

Ответ: 1.

5. Найти экстремумы функции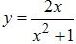

Найдем производную функции:

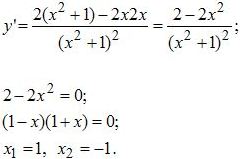
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2 и для третьего возьмём 2, тогда производная будет -0,24. И проставим соответствующие знаки.

Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет минимум, а при прохождении через 1 – меняет знак и плюса на минус, соответственно это будет максимум.

6. Найти экстремумы функции .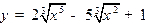

Дифференцируем:. Производная, очевидно, не существует при х =0. Кроме того, она равна 0 при х =1. Следовательно, имеем две стационарные точки х ₁=0 и х ₂=1. Опять используем первое достаточное условие:

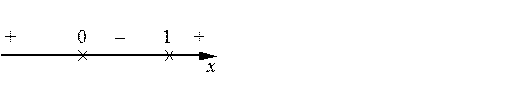
Здесь для определения знаков производной в интервалах вычислялись: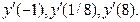

Таким образом, заданная функция имеет максимум при х =0 и минимум при х =1. Соответствующие экстремальные значения: у _max= f (0)=...=1, y _min= f (1)=...= –2.

Ответ: у _max=1, y _min= –2.

7. Найти экстремумы функции у = 3 – 2 х ² + х ⁴

Дифференцируем: .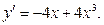

Стационарные точки: 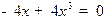, откуда ; .

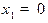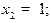
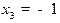Используем второе достаточное условие. Вторая производная: 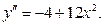. Таким образом:

,

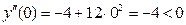т.е. 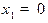является точкой максимума и

,

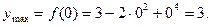
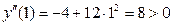т.е. 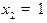является точкой минимума и

.

,

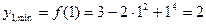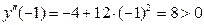т.е. 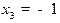является второй точкой минимума и

.

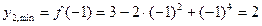8. Исследовать выпуклости функции у =3 х ⁴ – 4 х ³.

Дифференцируем: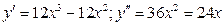

Стационарные значения для второй производной: 36 х ² – 24 х =0, откуда х ₁=0 и х ₂=

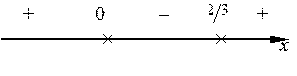
Вычисляя знаки второй производной в интервалах обычным образом, заключаем, что обе точки будут точками перегибов заданной функции, причем при х < 0 и х > 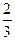функция вогнутая, а при 0 < x < 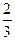функция выпуклая.

Ординаты точек перегиба: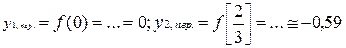

9. Исследовать функцию 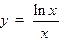и построить ее график.

· ОДЗ этой функции: x >0. Вертикальная асимптота: х =0.

· Уже по ОДЗ ясно, что заданная функция – общего вида.

· Определим точку пересечения с осью Ox: 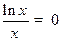, откуда 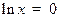и х = 1.

· Дифференцируем: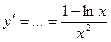

· Определим стационарные точки. Значение х =0 исключаем, как не вошедшее в ОДЗ. Тогда: 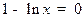, откуда х = е.

· Выберем второе достаточное условие.

Вторая производная: .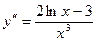

Тогда, 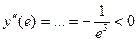т.е. точка х = е является точкой максимума и 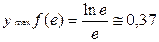. Заданная функция возрастает при x < e и убывает при x > e.

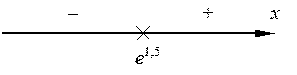
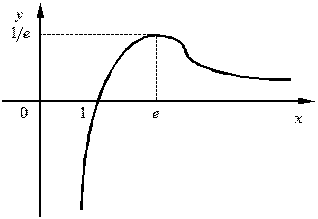
· Определим выпуклости заданной функции.Стационарные значения второй производной 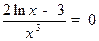, откуда х = е ^1,5. Таким образом, точка х = е ^1,5 является точкой перегиба, причем слева от нее функция выпукла, а справа – вогнута. Ордината у _пер.=...= .

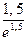· Проверим горизонтальную асимптоту:

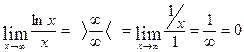, следовательно, ось оХ является горизонтальной асимптотой.

Вопросы для самоконтроля:

1. Правило Лопиталя.

2. Возрастание и убывание функций.

3. Необходимое условие экстремума.

4. Первое достаточное условие экстремума.

5. Второе достаточное условие экстремума.

6. Глобальные экстремумы.

7. Выпуклость и вогнутость функции.

8. Асимптоты.

9. Общая схема исследования функции и построение графиков.

Поиск по сайту: