 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Комплексные числа в алгебраической форме
Комплексным числом называется выражение вида
 , (10.1)
, (10.1)
(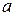 и
и  – действительные числа,
– действительные числа,  – мнимая единица), если для любых комплексных чисел
– мнимая единица), если для любых комплексных чисел  и
и  введены операции по следующим правилам:
введены операции по следующим правилам:
1) два комплексных числа  и
и  называются равными, если
называются равными, если  и
и 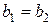 ;
;
2) суммой и разностью двух комплексных чисел 
и  называется комплексное число
называется комплексное число

 ; (10.2)
; (10.2)
3) произведением двух комплексных чисел  и
и  называется комплексное число
называется комплексное число
 . (10.3)
. (10.3)
Степени числа  :так как
:так как  то
то
 (10.4)
(10.4)
Запись комплексного числа в виде  называется алгебраической формой записи комплексного числа, где
называется алгебраической формой записи комплексного числа, где 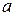 действительная часть числа
действительная часть числа 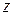 и обозначается
и обозначается  , а
, а  – мнимая часть числа
– мнимая часть числа 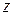 и обозначается
и обозначается  . Тогда комплексное число можно записать как
. Тогда комплексное число можно записать как 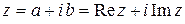 .
.
Любое действительное число 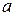 содержится во множестве комплексных чисел, его можно записать так:
содержится во множестве комплексных чисел, его можно записать так:  . Числа 0, 1,
. Числа 0, 1,  записываются соответственно в виде
записываются соответственно в виде  ,
,  ,
,  . Если
. Если  , комплексное число
, комплексное число  обращается в чисто мнимое число
обращается в чисто мнимое число  . Комплексное число
. Комплексное число  (отличается только знаком мнимой части) называется комплексно сопряженным с числом
(отличается только знаком мнимой части) называется комплексно сопряженным с числом 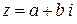 . Комплексные числа
. Комплексные числа  и
и  называются противоположными. Модулем комплексного числа
называются противоположными. Модулем комплексного числа 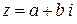 называют число
называют число  :
:
 . (10.5)
. (10.5)
Модуль комплексного числа всегда есть действительное неотрицательное число  , причем
, причем  тогда и только тогда, когда
тогда и только тогда, когда 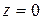 . Из определения модуля комплексного числа следует, что для любых комплексных чисел
. Из определения модуля комплексного числа следует, что для любых комплексных чисел  справедливы соотношения
справедливы соотношения
 ;
;  , если
, если  , (10.6)
, (10.6)
для любого целого числа 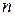 (при
(при  предполагается, что
предполагается, что  ).
).
 Каков геометрический образ комплексного числа
Каков геометрический образ комплексного числа 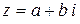 ? Комплексное число
? Комплексное число 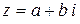 изображают на координатной плоскости точкой с декартовыми координатами
изображают на координатной плоскости точкой с декартовыми координатами  . Действительные числа
. Действительные числа 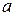 изображаются точками оси
изображаются точками оси  -ов. Чисто мнимые числа
-ов. Чисто мнимые числа  – точками
– точками
оси 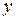 -ов. Ось
-ов. Ось  -ов – действительная ось. Ось
-ов – действительная ось. Ось 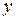 -ов – мнимая ось. Точка А
-ов – мнимая ось. Точка А  , соответствующая комплексному числу
, соответствующая комплексному числу  называется аффиксом данного комплексного числа.
называется аффиксом данного комплексного числа.
Каждой точке плоскости с координатами  соответствует один и только один вектор с началом в точке О (0,0)и концом в точке А
соответствует один и только один вектор с началом в точке О (0,0)и концом в точке А  . Поэтому комплексное число
. Поэтому комплексное число 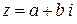 можно изобразить в виде вектора
можно изобразить в виде вектора  с началом в точке
с началом в точке 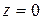 и концом в точке (рис. 10.2).
и концом в точке (рис. 10.2).
 Пример 1.Записать аффиксы следующих комплексных чисел и построить соответствующие им радиусы-векторы: 1)
Пример 1.Записать аффиксы следующих комплексных чисел и построить соответствующие им радиусы-векторы: 1)  2)
2)  3)
3)  ; 4)
; 4)  ; 5)
; 5)  .
.
Решение.
1) М 1(2, 0);
2) М 2(–3, 0);
3) М 3(0, 3);
4) М 4(0, –2);
5) М 5(2, 3) (рис. 10.1).
 Пример 2.Найти множество точек, для которых
Пример 2.Найти множество точек, для которых  .
.
Решение.Точки искомого множества удовлетворяют неравенству  , т. к.
, т. к.  (рис. 10.3).
(рис. 10.3).
Пример 3. Найти корни уравнения  .
.
Решение. По известной формуле имеем
 ,
,
т. е. 
Ответ: 
Пример 4. Найти сумму  , если: а)
, если: а)  и
и 
Решение.  =
=  .
.
Ответ:  .
.
Найти сумму  , если: б)
, если: б)  и
и  .
.
Решение.  =
=  .
.
Ответ:  .
.
Пример 5. Найти разность  , если
, если  и
и  .
.
Решение.  = (
= ( ) – (
) – ( ) =
) =  .
.
Ответ:  .
.
Пример 6. Найти  , если
, если  и
и  .
.
Решение.  =(
=( )
)  )=
)=  .
.
Ответ:  .
.
Пример 7. Найти  , если
, если  и
и  .
.
Решение.  =
=  .
.
Ответ:  .
.
Поиск по сайту: