 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тренировочные задачи
Вычислить пределы:
· 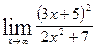 .
.
Ответ: 4,5
·  .
.
Ответ: 0
· 
Ответ: 1
· 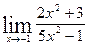
Ответ: 1,25
· 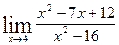
Ответ: 0,125
· 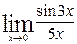
Ответ: 0,6
Лекция 6. Производная и дифференциал функции
Вопросы для изучения:
1.Определения. Геометрический и физический смысл.
2.Табличные производные.
3. Производная сложной функции.
4. Логарифмическое дифференцирование.
Определения. Геометрический и физический смысл

Приращением функции у=f(x) в интервале Dх называется разность D у=f(х+Dх)-f(x). Если D у >0, то функция на интервале возрастает; при D у <0 - убывает; при D у =0 – не изменяется.
Предел отношения приращения функции D у к приращению аргумента D х при стремлении D х к нулю называется производной функции:

Другие, эквивалентные, обозначения:
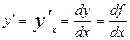

Геометрический смысл производной тесно связан с понятием касательной.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
С физической точки зрения производная - скорость изменения функции в данной точке.
Если функция имеет единственную производную в точке, она называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала a  ,
,  называется дифференцируемой в данном интервале.
называется дифференцируемой в данном интервале.
Табличные производные
С помощью определения можно вычислять производные функций. Пример:
y= f(x)=x2  f(x+
f(x+  x)=(x+
x)=(x+ 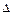 x)2=x2+2x
x)2=x2+2x 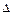 x+(
x+( 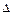 x)2
x)2 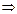
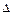 y=
y=
f(x+ 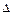 x) - f(x)=2x
x) - f(x)=2x 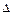 x+(
x+( 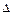 x)2.
x)2.
Отсюда  и
и 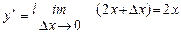
Совершенно аналогично можно получить и производные любых других функций. На этой основе разработана и постоянно используется стандартная таблица производных:

Теоремы дифференцирования
Так же, как и при вычислении пределов, математика разработала ряд теорем, ускоряющих вычислительную работу. Приведем их без доказательств:
· Сумма: у=u(x) 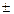 v(x)
v(x) 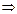
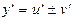 .
.
· Произведение: y=u 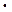 v
v 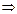
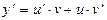 .
.
· Частное: y= 

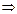
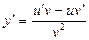
· Постоянный множитель: y=Cu 


Поиск по сайту: