АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определители и системы линейных уравнений

Читайте также:
  1. B. Взаимодействие с бензодиазепиновыми рецепторами, вызывающее активацию ГАМК – ергической системы
  2. CRM системы и их возможности
  3. IV. Поземельные книги и другие системы оглашений (вотчинная и крепостная системы)
  4. Автокорреляция в остатках. Критерий Дарбина-Уотсона в оценке качества уравнений, построенных по временным рядам.
  5. Автоматизированное рабочее место (АРМ) таможенного инспектора. Назначение, основные характеристики АРМ. Назначение подсистемы «банк - клиент» в АИСТ-РТ-21.
  6. Автоматизированные информационно-поисковые системы
  7. Автоматизированные системы бронирования, управления перевозками, отправками в аэропортах.
  8. Автоматизированные системы управления воздушным движением.
  9. Автоматические системы пожаротушения.
  10. Адекватность понимания связи свойств нервной системы с эффективностью деятельности
  11. Анализ активности вегетативной нервной системы
  12. Анализ деятельности и системы управления персоналом

Рассмотрим систему из двух уравнений первого порядка:

Выделим из этой системы три определителя:

определитель самой системы D= ,

определитель для первого неизвестного D1= ,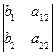

определитель для второго неизвестного D2= .

Обратим внимание, что индексы у определителей для неизвестных будут теперь соответствовать номеру неизвестного в системе. Рассмотрим три возможных случая:

 

1. Определитель системы D 0. Тогда имеем единственное решение х1 = , х2 = (формулы Крамера для двух неизвестных).

2. D=D1=D2=0. В этом случае система имеет бесконечное множество решений.

3. D=0, но D1 или D2, или оба вместе, не равны нулю. В этом случае система несовместна, т.е. не имеет никаких решений.

Совершенно аналогично строятся формулы Крамера для систем более высокого порядка. Так, для трех уравнений:

D= ,
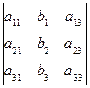D1= , D2= , D3= .

Тогда, если D 0, то единственное решение определится формулами хi = (i =1, 2, 3).

Так же, как и при вычислении определителей, формулы Крамера, из-за арифметических трудностей, используются на практике для систем не выше третьего - четвертого порядков.

 

Примеры решения задач

1.Вычислить определитель D 2= .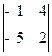

 

Решение:

 

Ответ: 18.

2.Вычислить определитель D 2= .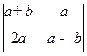

 

Ответ: .

3.Решить уравнение

 

Раскроем: .

Следовательно, имеем уравнение: x 2+5 x +4=0, откуда .

Ответ:{–4; –1}.

4. Вычислить определитель .

Раскроем по первой строке:

=

Ответ: 0.

5. Вычислить определитель .

Так как определитель треугольный, то его значение равно произведению элементов главной диагонали. Следовательно:.

Ответ: –36.

6.Вычислить определитель .

Здесь удобно выбрать вторую строку, т.к. два нуля сокращают вычисления.

.

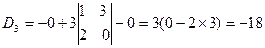Ответ: –18.

7. Решить по формулам Крамера систему уравнений

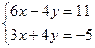
Вычислим все определители:

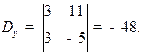
Тогда

Ответ: .

8. Решить по формулам Крамера систему уравнений

Вычислим:



Тогда

Ответ: {1; 2; 3}.

Вопросы для самоконтроля:

1. Определитель второго порядка.

2. Минор, адъюнкт.

3. Определители третьего и n –го порядков.

4. Общая формула вычисления определителей.

5. Основные свойства определителей.

6. Формулы Крамера для систем линейных уравнений.

7. Несовместность системы линейных уравнений.

8. Бесконечное множество решений системы линейных уравнений.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)