Общее уравнение прямой линии

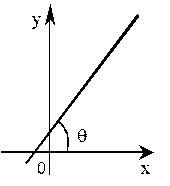
Общее уравнение прямой линии имеет вид А х +В у +С=0 где А, В, С 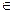R. Другая форма записи (нормализованное уравнение) у =к х +b, где , 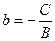Отметим, что к=tg , где - угол наклона

прямой к оси Х. Придавая нулевые значения коэффициентам, получим варианты общего уравнения:

А=0: В у +С= 0 или у =b - прямая, параллельная оси оx;

В=0: А х +С=0 или прямая, параллельная оси оy;

С=0: А х +В у =0 или у =к х - прямая проходит через начало координат;

А=В=С=0 - вырождение прямой.

Таким образом, всякое невырожденное уравнение первой степени Ах+Ву+С=0 при является уравнением прямой линии на плоскости.

Если на плоскости имеются две прямые А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0, то их взаимодействие описывается четырьмя случаями:

·  Точка пересечения прямых определится из системы уравнений:

или .

·  Если прямые параллельны, то соблюдается условие:

к₁=к_2.

·  Если прямые перпендикулярны, то соблюдается условие:

А₁А₂+В₁В₂=0 или .

·  Угол между прямыми определится из условия:

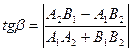или

Здесь знак модуля взят для обеспечения положительного результата.

Варианты уравнения прямой

На практике часто встречаются случаи, когда надо получить уравнение прямой не только с помощью приведенных выше общего и нормализованного уравнений. Рассмотрим некоторые такие случаи.

1. Известно, что прямая образует с оХ угол и проходит через известную точку М(а; b). Найти уравнение (прямая через точку по заданному направлению).

Так как известно, то к=tg . Тогда уравнение прямой

Это уравнение легко преобразуется в уже известные формы записи.6,

2. Известны точки М(а; b) и N(c; d). Найти уравнение проведенной через них прямой (прямая через две точки).

Из прямоугольного треугольника MNP определяем

Тогда

После преобразования получим

= .

Если а=с или b =d, то следует использовать другую форму записи:

(х-а)(d-b)=(y-b)(c-a).

3. Известны отрезки а и b, которые прямая отсекает от осей координат. Найти уравнение этой прямой (уравнение прямой в отрезках).

Искомое уравнение имеет вид

.

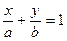Отметим, что, если прямая параллельна оси ОХ или ОY, то такое уравнение составить нельзя - нет отрезка.

Построение прямых. Расстояния

Приведем некоторые типовые задачи, часто встречающиеся в практике.

1. Пусть известна прямая Ах+Ву+С=0 (или у=кх+b) и требуется провести новую прямую, проходящую через точку М(c; d) параллельно данной.

Искомое уравнение имеет вид:

A(x-c)+B(y-d)=0

или y-d=k(x-c),

где к уже известно.

2. Пусть известна прямая Ах+Ву+С=0 (или у=кх+b) и требуется провести новую прямую, проходящую через точку М(c; d) перпендикулярно данной.

Искомое уравнение имеет вид

или

.

3. Требуется определить расстояние между точками М(a; b) и N(c;d).

Задача решается с помощью теоремы Пифагора. Искомая формула имеет вид (длина отрезка):

l = .

4. Известны прямая Ах+Ву+С=0 (или у=кх+b) и точка N(c; d), не лежащая на этой прямой. Требуется определить расстояние от точки до данной прямой.

Искомая формула имеет вид

или

Модуль - для обеспечения положительного

Примеры решения задач

Функция – основной аналитический описатель различных процессов. Рассмотрим ряд примеров, раскрывающих важные стороны этого базового понятия.

1 Найти область определения (ОДЗ) функции .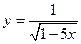

На множестве R следует выполнить условие:

, т.е. или х < 0,2.

Ответ: .

2. Найти ОДЗ функции .

Так как на ноль делить нельзя, то следует выполнить условие

Ответ: .

3. Исследовать на четность функцию .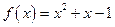

Положим х₁ = 2, х₂ = –2. Тогда и . Так как корреляции типов или 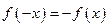не устанавливается, следовательно, заданная функция – общего вида.

4. Исследовать на четность функцию .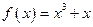

Принимая те же значения, что и в примере 3, имеем:

и .

Так как 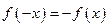, то заданная функция – нечетная.

5. Представить сложную функцию системой.

Решение: .

6. Представить сложную функцию системой.

Решение: .

8. Определить точку пересечения прямых и .

Система уравнений.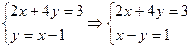

Решая систему, получим , что и является искомой точкой.

9. Составить уравнение прямой, проходящей через точку 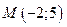параллельно прямой .

Искомое уравнение определяется формулой

, т.е. .

Отсюда .

10. Составить уравнение прямой, проходящей через точку 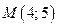перпендикулярно к прямой .

Используем условие перпендикулярности

.

Тогда или , откуда .

11. Составить уравнение прямой, проходящей через две точки (1; 5) и (3; 9).

Используем уравнение прямой, проходящей через две точки:

, т.е. .

Отсюда .

12. Прямую привести к уравнению в “отрезках”.

Вычислим отрезки: при y= 0 x= – 4 = a – отрезок по оси оX, при x= 0 y= 6= b – отрезок по оси оY. Тогда искомое уравнение

.

Вопросы для самоконтроля:

1. Определение функции.

2. Области определения и значений функции.

3. Способы задания функции.

4. Возрастание и убывание функции.

5. Периодическая функция.

6. Основные элементарные функции.

7. Алгебраические и трансцендентные функции.

8. Неявная функция. Сложная функция.

9. Общее уравнение прямой линии и его варианты.

10. Взаимодействие двух прямых линий.

11. Уравнение прямой, проходящей через точку по заданному направлению.

12. Уравнение прямой, проходящей через две точки.

13. Уравнение прямой в “отрезках”.

14. Угол между прямыми линиями.

15. Параллельность и перпендикулярность прямых.

16. Расстояние от точки до прямой.

Поиск по сайту: