 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Непрерывность и разрывы функции
Функция f(x) называется непрерывной в точке x0 если она:
· Определена в этой точке, т.е. существует f(x0).
· Имеет предел в этой точке 
· Пределсовпадает со значением функции А= f(x0).
Если хотя бы одно из этих условий нарушено, то функция разрывная в точке x0. Этот разрыв может быть конечен - скачок (разрыв первого рода), или бесконечен (второго рода).
Для функций, непрерывных в точке x0 сумма f1+f2, произведение f1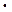 
f2 и частное 
(при f2 ¹0) также непрерывны в этой точке.
Если функция y= f1(u) непрерывна в точке u0, а функция u= f2(x) непрерывна в точке f2(x0), то, при u0= f2(x0), сложная функция f1(f2(x)) тоже непрерывна в этой точке, т.е. можно записать: 
Функция y= f(x) называется непрерывной на интервале a 
x b, если она непрерывна в каждой точке этого интервала. При этом:
· Она ограничена на этом интервале сверху и снизу (не может быть бесконечного значения).
· Обязательно имеет минимальное и максимальное значения.
· Если по концам интервала функция имеет разные знаки, то внутри интервала имеется хотя бы одна точка х=с, в которой f(с)=0 (корень функции).
Примеры решения задач
Понятие предела позволяет прогнозировать поведение различных процессов или моделей как на бесконечности, так и в конкретных точках. На ряде примеров покажем основные методы вычисления пределов.
1. 
.
В любой задаче на пределы сначала рассматривается прямая подстановка 
. Если при этом получается конечное значение (в том числе и 0), то расчет закончен. В данном примере 
Ответ: 13.
2.. 
Решение: 
Ответ: 0.
3. 
.
Решение: 
.
Ответ: 1.
4.. 
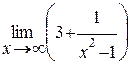
Решение: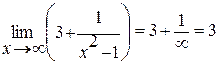 
Здесь использована теорема: величина, обратная бесконечно большой, является бесконечно малой, т.е. 0.
5. 
.
Решение: 
.
В данном случае прямая подстановка привела к неопределенности. Попробуем упростить функцию:
.
Таким образом,
.
Ответ: 0
6. 
Решение: 
.
Используем разложение квадратного трехчлена на множители по известной формуле: 
, где 
.
Тогда. 
Следовательно,. 
Ответ: 0,5625.
7. 
.
Решение: 
В этом случае следует разделить числитель и знаменатель на старшую степень аргумента, т.е. на х 3, и использовать теорему 
, т.е.
Ответ: 
8.. 
Решение: 
Ответ: функция – бесконечно большая при 
.
9. 
.
Вспомним первый замечательный предел 
.
Для приведения заданного выражения к такому виду введем замену переменной: u =3 x; отсюда 
.
Следовательно, 
Для аргумента: 
, т.е. 
или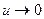 
.
Таким образом, 
.
Ответ: 3.
10. 
Используем второй замечательный предел в форме: 
.
Заменяем переменную: 
, откуда 
и 
. Из 
следует 
и 
. Таким образом: 
Ответ: е 2.
11. 
Используем второй замечательный предел в форме: 
.
Заменяем переменную: 
, откуда 
. Из следует 
и .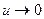
Таким образом: 
.
Ответ: 
.
Вопросы для самоконтроля:
1. Определение предела переменной величины.
2. Определение предела функции.
3. Бесконечно малые (б.м.) и бесконечно большие (б.б.) величины.
4. Свойства б.м. и б.б. величин.
5. Теоремы о пределах.
6. Замечательные пределы.
7. Методы вычисления пределов.
8. Непрерывность функции в точке и на интервале.
9. Свойства функций, непрерывных в точке.
10. Непрерывность сложной функции.
11. Типы разрывов функции.
12. Свойства функций, непрерывных на интервале.
Поиск по сайту: