 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основные определения и понятия
Частный случай матрицы, состоящей из одного столбца, имеет широкое самостоятельное применение. Геометрическое изображение вектора направленным отрезком, известное из школьного курса, можно определить как совокупность проекций вектор-отрезка, записанных в виде матрицы-столбца. Тогда имеем понятие свободного вектора, не зависящего от точки приложения, которая может быть как в начале координат (радиус-вектор), так и в любой точке пространства. Направление вектора всегда строго сохраняется. Для двумерного случая: 
 или
или  ;
; 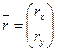 или
или  . Для общности, все проекции в дальнейшем обозначаются через х
. Для общности, все проекции в дальнейшем обозначаются через х 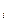 и называются координатами вектора. Если какая-то проекция х
и называются координатами вектора. Если какая-то проекция х 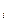 отрицательна, то она откладывается в противоположную сторону соответствующей оси координат.
отрицательна, то она откладывается в противоположную сторону соответствующей оси координат.
Совершенно так же выглядят векторы  =
=  в трехмерной системе координат - добавляется координата z. Но векторы размерности более трех наглядно не представимы - они могут быть поняты только по аналогии. Общее определение: вектором в n -мерном пространстве называется упорядоченный набор n координат
в трехмерной системе координат - добавляется координата z. Но векторы размерности более трех наглядно не представимы - они могут быть поняты только по аналогии. Общее определение: вектором в n -мерном пространстве называется упорядоченный набор n координат  =
=  , число которых равно размерности пространства, т.е. n.
, число которых равно размерности пространства, т.е. n.
Длина вектора определяется формулой d =  . Все операции с векторами - те же, что и матрицами.
. Все операции с векторами - те же, что и матрицами.
Рассмотрим линейную комбинацию трех векторов: k 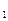

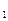 +k
+k 

 +k
+k 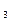

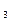 .
.
Если равенство k 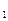

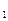 +k
+k 

 +k
+k 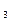

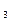 =0 возможно только при k
=0 возможно только при k 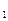 =k
=k  =k
=k 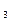 =0, то векторы
=0, то векторы 
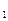 ,
, 
 и
и 
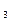 называются линейно независимыми. Иначе, по крайней мере, один из векторов можно выразить суммой двух других и векторы будут линейно зависимыми. Например, при k
называются линейно независимыми. Иначе, по крайней мере, один из векторов можно выразить суммой двух других и векторы будут линейно зависимыми. Например, при k 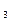
 0 можно записать:
0 можно записать: 
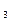 =
=  (- k
(- k 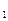

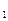 - k
- k 

 ).
).
Максимально возможное число линейно независимых векторов равно размерности пространства. Так, для плоскости возможны только два таких вектора, для прямой - один. Для n- мерного пространства число векторов равно n.
Пусть на плоскости имеются векторы  ,
,  и
и  . Покажем, что они линейно зависимы. Составим их линейную комбинацию:
. Покажем, что они линейно зависимы. Составим их линейную комбинацию:  и перейдем к алгебраической форме:
и перейдем к алгебраической форме:

 .
.
Таким образом, положив k 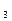 =1, имеем:
=1, имеем:  или
или 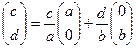 , т.е. третий вектор не является независимым и выражается суммой двух других или разлагается по двум другим векторам. Рассмотрим первые два вектора подробнее:
, т.е. третий вектор не является независимым и выражается суммой двух других или разлагается по двум другим векторам. Рассмотрим первые два вектора подробнее:  и
и  . Тогда
. Тогда  - очень компактная запись через единичные векторы (или орты). Покажем, что орты линейно независимы: k
- очень компактная запись через единичные векторы (или орты). Покажем, что орты линейно независимы: k 
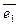 + k
+ k 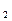
 =
=  или
или  , откуда k
, откуда k  =k
=k 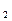 = 0.
= 0.
Так как с и d произвольны, то, очевидно, любой вектор на плоскости можно представить комбинацией двух ортов 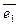 и
и  . Это называется разложением вектора по единичному базису или, точнее, по ортонормированному, т.к. длина каждого орта равна 1. Конечно, можно разлагать не по ортам, а по двум любым линейно независимым векторам (по общему базису), к примеру,
. Это называется разложением вектора по единичному базису или, точнее, по ортонормированному, т.к. длина каждого орта равна 1. Конечно, можно разлагать не по ортам, а по двум любым линейно независимым векторам (по общему базису), к примеру,  и
и  , но разложение с помощью ортов является и простым, и общим.
, но разложение с помощью ортов является и простым, и общим.
Все введенные выше понятия справедливы для пространства любой размерности. В n -мерном пространстве всегда имеются n линейно независимых ортов 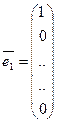 ,
,  ,...,
,...,  , поэтому любой вектор
, поэтому любой вектор  можно разложить по ортонормированному базису:
можно разложить по ортонормированному базису:  = а1
= а1 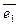 +а2
+а2  +...+аn
+...+аn  . Разложение векторов по базису из линейно независимых векторов всегда единственно в любом принятом базисе.
. Разложение векторов по базису из линейно независимых векторов всегда единственно в любом принятом базисе.
Поиск по сайту: