АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема о среднем определенного интеграла

Читайте также:
  1. В) в среднем каждая денежная единица евро обращается пять раз в год,
  2. Вычисление двойного интеграла в декартовых координатах
  3. Вычисление площади с помощью криволинейного интеграла второго рода.
  4. Задача о массе неоднор.тела.Опр-ние тройного интеграла
  5. Короткого времени (в среднем 8,3 года). За это время в своем
  6. Место наречий неопределенного времени в предложении
  7. Модель IS-LM открытой экономики. Теорема Манделла-Флеминга.
  8. Напоминаем, что Present Perfect употребляется в предложениях, в которых время выражено наречиями неопределенного времени.
  9. Обобщённая модель регрессии. Обобщённый метод наименьших квадратов. Теорема Айткена
  10. Определение криволинейного интеграла второго рода.
  11. Определение криволинейного интеграла первого рода.
  12. Основная теорема антагонистических игр Джона фон Неймана и седловая точка функции выигрыша.

Прикладное значение теоремы о среднем заключается в возможности получения качественной оценки значения определенного интеграла без его вычисления. Формулируем: если функция 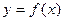непрерывна на интервале 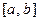, то внутри этого интервала найдется такая точка 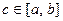, что .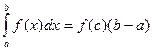

 
 
 

 

 

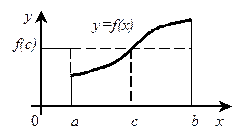
Геометрический смысл этой теоремы заключается в том, что внутри интервала интегрирования всегда найдется такая точка , что площадь криволинейной трапеции будет равна площади прямоугольника со сторонам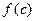и и .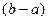

 

Эта формула вполне пригодна для прикидочной оценки интеграла от сложной или громоздкой функции. Единственным моментом, который делает формулу приближенной, является необходимость самостоятельного выбора точки . Если принять наиболее простой путь – середину интервала интегрирования 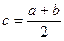(как предлагается в ряде учебников), то ошибка может быть весьма значительной. Для получения более точного результата рекомендуем провести расчет в следующей последовательности:

1)построить график функции 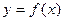на интервале ;

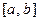2) провести верхнюю границу прямоугольника таким образом, чтобы отсекаемые части графика функции 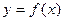были примерно равны по площади (именно так показано на вышеприведенном рисунке – два криволинейных треугольника практически одинаковы);

3) определить из рисунка ;

4) воспользоваться теоремой о среднем.

В качестве примера вычислим простой интеграл :

и приближенное значение 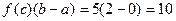, т.е. явно неточный результат.

 

Построив график с проведением верхней стороны прямоугольника в соответствии с рекомендациями, получим 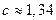, откуда 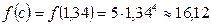и приближенное значение 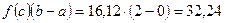. Вполне удовлетворительный результат, точное значение .

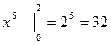Для середины интервала получим 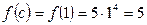и приближенное значение ,т.е. явно неточный результат. Построив график с проведением верхней стороны прямоугольника в соответствии с рекомендациями, получим ,откуда 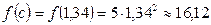и приближенное значение 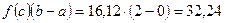. Впольне удовлетворительный результат, погрешность составляет 0,75%.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)