 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вещественные числа
Арифметический сопроцессор может работать либо с данными в формате с плавающей точкой, либо с целыми числами.
Перед тем как приступить к изучению форматов вещественных чисел, используемых сопроцессором, вспомним о числах с плавающей точкой, встречающихся в научных расчетах.
В общем виде эти числа можно записать следующим образом:
(знак)(мантисса)*10(знак)(порядок)
Например: -1.35*105. Здесь знак - это минус, мантисса - 1.35, порядок - 5. Порядок тоже может иметь знак.
Вспомним нормализованное представление чисел: если целая часть мантиссы числа состоит из одной цифры, не равной нулю, то число с плавающей точкой называется нормализованным.
Преимущества использования нормализованных чисел в том, что для фиксированной разрядной сетки числа (то есть для фиксированного количества цифр в числе) нормализованные числа имеют наибольшую точность. Кроме того, нормализованное представление исключает неоднозначность - каждое число с плавающей точкой может быть представлено различными (ненормализованными) способами:
123.5678*105 = 12.35678*106 = 1.235678*107 = 0.1235678*108 и т.д.
Для тех, кто программировал на языках высокого уровня, знакомо следующее представление чисел с плавающей точкой:
(знак)(мантисса)E(знак)(порядок)
Например, -5.35E-2 означает число -5.35*10-2. Такое представление называется научной нотацией.
Арифметический сопроцессор может работать с вещественными числами в трех форматах:
- одинарной точности;
- двойной точности;
- расширенной точности
Эти числа занимают в памяти, соответственно, 4, 8 или 10 байт (рис.1).

Рис. 1. Различные представления вещественных чисел
В любом представлении старший бит определяет знак вещественного числа: 0 - положительное число, 1 - отрицательное число.
Все равные по абсолютному значению положительные и отрицательные числа отличаются только этим битом. В остальном числа с разным знаком полностью симметричны. Для представления отрицательных чисел здесь не используется дополнительный код, как это сделано в центральном процессоре.
Арифметический сопроцессор работает с нормализованными числами, поэтому поле мантиссы содержит мантиссу нормализованного числа.
Так как здесь используется двоичное представление чисел, сформулируем определение нормализованного числа для двоичного представления: если целая часть мантиссы числа в двоичном представлении равна 1, то число с плавающей точкой называется нормализованным.
Так как для нормализованного двоичного числа целая часть всегда равна единице, то эту единицу можно не хранить. Именно так и поступили разработчики арифметического сопроцессора - в форматах одинарной и двойной точности целая часть мантиссы не хранится. Таким образом экономится один бит памяти.
Для наглядности представим мантиссу числа в следующей форме: n.nnnnnnnnnn...n
Здесь символом n обозначается либо 0, либо 1. Нормализованные числа в самой левой позиции содержат 1, поэтому их можно изобразить еще и в таком виде:
1.nnnnnnnnnn...n
Представление с расширенной точностью используется сопроцессором для выполнения всех операций. И даже более - все операции с числами сопроцессор выполняет над числами только в формате с расширенной точностью. В этом формате хранится и "лишний" бит целой части нормализованного числа.
Основная причина использования для вычислений расширенной точности - предохранение программы от возможной потери точности вычислений, связанной с большими различиями в порядках чисел, участвующих в арифметических операциях.
Поле порядка - это степень числа 2, на которую умножается мантисса, плюс смещение, равное 127 для одинарной точности, 1023 - для двойной точности и 16383 - для расширенной точности.
Для того, чтобы определить абсолютное значение числа с плавающей точкой, можно воспользоваться следующими формулами:
Одинарная точность: 1.(цифры мантиссы)*2(P-127)
Двойная точность: 1.(цифры мантиссы)*2(P-1023)
Расширенная точность: 1.(цифры мантиссы)*2(P-16383)
Знак числа, как мы уже говорили, определяется старшим битом.
Пример. Пусть мы имеем число с одинарной точностью, которое в двоичном виде выглядит следующим образом: 1 01111110 11000000000000000000000
Для этого числа знаковый бит равен 1 (отрицательное число), порядок равен 126, мантисса - 11 (в двоичной системе счисления). Значение этого числа равно:
1.11 * 2(126-127) = -1.75 * 2-1 = -0,875
Рассмотрим теперь особые случаи представления вещественных чисел.
Нуль - это такое число, у которого порядок и мантисса равны нулю. Нуль может иметь положительный или отрицательный знаки, которые игнорируются в операциях сравнения. Таким образом, имеется два нуля - положительный и отрицательный.
Наименьшее положительное число - это число, которое имеет нулевой знаковый бит, значение порядка, равное 1, и значение мантиссы, равное нулю. В зависимости от представления наименьшее положительное число имеет следующие значения: 1,17*10-38 (одинарная точность), 2.23*10-308 (двойная точность), 3.37*10-4932 (расширенная точность).
Наибольшее отрицательное число - полностью совпадает с наименьшим положительным числом, но имеет бит знака, установленный в 1.
Наибольшее положительное число - это число, которое имеет нулевой знаковый бит, поле порядка, в котором все биты кроме самого младшего, равны 1, и содержит единицы во всех разрядах мантиссы. В зависимости от представления наибольшее положительное число имеет следующие значения: 3.37*1038 (одинарная точность), 1.67*10308 (двойная точность), 1.2*104932 (расширенная точность).
Наименьшее отрицательное число - полностью совпадает с наибольшим положительным числом, но имеет бит знака, установленный в 1.
Положительная и отрицательная бесконечность - это число содержит все единицы в поле порядка и все нули в поле мантиссы. В зависимости от состояния знакового бита может быть положительная и отрицательная бесконечности. Бесконечность может получиться, например, как результат деления конечного числа на нуль.
Нечисло - содержит все единицы в поле порядка и любое значение в поле мантиссы. Нечисло может возникнуть в результате выполнения неправильной операции при замаскированных особых случаях.
Неопределенность - содержит в поле порядка все единицы, а в поле мантиссы - число 1000..0 (для одинарной и двойной точности) или 11000..0 (для расширенной точности, так как в этом формате хранится старший бит мантиссы).
Для большей наглядности сведем все возможные представления вещественных чисел вместе на рис. 2.

Рис. 2. Возможные представления вещественных чисел
Целые числа
Арифметический сопроцессор наряду с вещественными числами способен обрабатывать и целые числа. Он имеет команды, выполняющие преобразования целых чисел в вещественные и обратно.
Возможно четыре формата целых чисел:
- целое число;
- короткое целое число;
- длинное целое число;
- упакованное десятичное число.
Целое число занимает 2 байта. Его формат полностью соответствует используемому центральным процессором. Для представления отрицательных чисел используется дополнительный код. Короткое целое и длинное целое имеют аналогичные форматы, но занимают, соответственно, 4 и 8 байт.
Упакованное десятичное число занимает 10 байт. Это число содержит 18 десятичных цифр, расположенных по две в каждом байте. Знак упакованного десятичного числа находится в старшем бите самого левого байта. Остальные биты старшего байта должны быть равны 0.
Существуют команды сопроцессора, которые преобразуют числа в формат упакованных десятичных чисел из внутреннего представления в расширенном вещественном формате. Если программа делает попытку преобразования в упакованный формат ненормализованных чисел, нечисел, бесконечности и тому подобных, в результате получается неопределенность. Неопределенность в упакованном формате представляет из себя число, в котором два старших байта содержат единицы во всех разрядах. Содержимое остальных восьми байтов произвольно. При попытке использовать такое упакованное число в операциях фиксируется ошибка.
Для вещественных чисел для представления отрицательных чисел используется специальный знаковый бит. Для целых чисел используется дополнительный код.
В дополнительном коде положительные числа содержат нуль в самом старшем бите числа: 0XXX XXXX XXXX XXXX
Для получения отрицательного числа в дополнительном коде из положительного надо инвертировать каждый бит числа и затем прибавить к числу единицу.
Например, число +5 в дополнительном коде выглядит следующим образом:
0000 0000 0000 0101 = +5
Для получения числа -5 вначале инвертируем значение каждого бита:
1111 1111 1111 1010
Теперь прибавим к полученному числу +1: 1111 1111 1111 1011 = -5
На рис. 3 приведены все возможные варианты представления целых чисел.
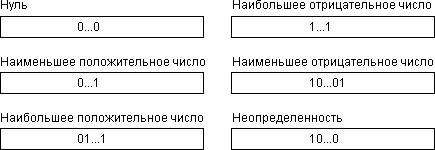
Рис. 3. Возможные представления целых чисел
Формат упакованного десятичного числа показан на рис. 4.

Рис. 4. Формат упакованного десятичного числа
На этом рисунке n0...n17 означают разряды десятичного числа. Они могут изменяться в пределах от 0000 до 1001, то есть от 0 до 9 в десятичной системе счисления.
Поиск по сайту: