Лабораторная работа №3. Способы измерения информации

Способы измерения информации

В основе теории информации лежит предложенный Шенноном способ измерения количества информации, содержащейся в одной случайной величине, относительно другой случайной величины, Этот способ приводит к выражению количества информации числом.

Для дискретных случайных величин X и Y, заданных законами распределения , 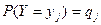и совместным распределением , количество информации, содержащейся в X относительно Y, равно

, (1)

Для непрерывных величин X и Y, заданных плотностями вероятностей и , аналогичная формула имеет вид

. (2)

Энтропия

Для дискретных случайных величин X и Y, заданных законами распределения , 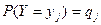и совместным распределением , энтропия определяется по формуле

. (3)

Для непрерывных величин X и Y, заданных плотностями вероятностей и , аналогичная формула имеет вид

. (4)

Связь между количеством информации и энтропией

, (5)

где .

Свойства количества информации и энтропии

1.

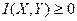
2. X и Y – независимы

3.

4. Х – константа

5. , где

6. . Если , то X – функция от Y. Если X – инъективная функция от Y (т.е. на разных значениях аргумента, она принимает разные значения), то .

Пример

Пусть дискретная случайная величина Х равна количеству очков, выпавших на игральной кости, а дискретная случайная величина Y равна 0, если выпавшее количество очков нечетно, и 1, если – четно.

Законы соответствующих случайных величин имеют вид:

Тогда закон совместного распределения будет иметь вид:

Тогда

Выводы: Точное количество выпавших очков дает точную информацию о четности. Из равенства следует, что информация об X полностью определяет Y, но не наоборот, т.к. . Действительно, Y функционально зависит от X, а X от Y функционально не зависит.

Задания

Найти количество информации и энтропию следующих случайных величин:

1. Х - результат двух подбрасываний идеальной монеты; Y – суммарное количество гербов.

2. Х - результат двух подбрасываний идеальной монеты; Y=1, если выпал ровно 1 герб, и Y=0 в противном случае.

3. Х - результат двух подбрасываний идеальной монеты; Y=1, если выпало ровно 2 герба, и Y=0 в противном случае.

4. Х - результат двух подбрасываний идеальной монеты; Y=1, если выпал хотя бы 1 герб, и Y=0 в противном случае.

5. Х – результат подбрасывания правильного шестигранника; Y=1, если количество выпавших очков >1, и Y=0 в противном случае.

6. Х – результат подбрасывания правильного шестигранника; Y=1, если количество выпавших очков >2, и Y=0 в противном случае.

7. Х – результат подбрасывания правильного шестигранника; Y=1, если количество выпавших очков >3, и Y=0 в противном случае.

8. Х – результат подбрасывания правильного шестигранника; Y=1, если количество выпавших очков >4, и Y=0 в противном случае.

9. Х – результат подбрасывания правильного шестигранника; Y=1, если количество выпавших очков >5, и Y=0 в противном случае.

10. Х – результат подбрасывания правильного шестигранника; Y= [(X+1)/2].

11. Х – результат подбрасывания правильного четырехгранника; Y=1, если количество выпавших очков >1, и Y=0 в противном случае.

12. Х – результат подбрасывания правильного четырехгранника; Y=1, если количество выпавших очков >2, и Y=0 в противном случае.

13. Х – результат подбрасывания правильного четырехгранника; Y=1, если количество выпавших очков >3, и Y=0 в противном случае.

14. Х – результат подбрасывания правильного четырехгранника; Y=1, если количество выпавших очков четное, и Y=0 в противном случае.

15. Х – результат случайного выбора карты из колоды в 36 карт; Y=1, если вытянута цифра, и Y=0 в противном случае.

16. Х – результат случайного выбора карты из колоды в 36 карт; Y=1, если вытянута картинка, и Y=0 в противном случае.

17. Х – результат случайного выбора карты из колоды в 36 карт; Y=1, если вытянута карта красной масти, и Y=0 в противном случае.

18. Х – результат случайного выбора двух карт из колоды в 36 карт; Y – количество карт красной масти.

19. Х – результат случайного выбора двух карт из колоды в 36 карт; Y – количество карт трефовой масти.

20. Х – результат случайного выбора двух карт из колоды в 36 карт; Y – количество карт с цифрами.

21. Х – результат случайного выбора двух карт из колоды в 36 карт; Y – количество карт с картинками.

22. Х – результат случайного выбора двух карт из колоды в 36 карт; Y=1, если вытянута ровно 1 карта бубновой масти, и Y=0 в противном случае.

23. Х – результат случайного выбора двух карт из колоды в 36 карт; Y=1, если вытянута ровно 2 карты червовой масти, и Y=0 в противном случае.

24. Х – результат случайного выбора двух карт из колоды в 36 карт; Y=1, если вытянута хотя бы 1 карта пиковой масти, и Y=0 в противном случае.

25. Х – результат случайного выбора двух карт из колоды в 36 карт; Y=1, если вытянута хотя бы 1 карта с цифрой, и Y=0 в противном случае.

26. Х – результат случайного выбора двух карт из колоды в 36 карт; Y=1, если вытянута ровно 1 карта с цифрой, и Y=0 в противном случае.

27. Х – результат случайного выбора двух карт из колоды в 36 карт; Y=1, если вытянута ровно 2 карты с цифрой, и Y=0 в противном случае.

28. Х – результат случайного выбора карты из колоды в 36 карт; Y=1, если вытянута карта бубновой масти, Y=2, если вытянута карта червовой масти, Y=3, если вытянута карта трефовой масти, Y=4, если вытянута карта пиковой масти.

Поиск по сайту: