 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Сжатие информации. Алгоритм Шеннона-Фэно
Цель сжатия - уменьшение количества бит, необходимых для хранения или передачи заданной информации, что дает возможность передавать сообщения более быстро и хранить более экономно и оперативно (последнее означает, что операция извлечения данной информации с устройства ее хранения будет проходить быстрее, что возможно, если скорость распаковки данных выше скорости считывания данных с носителя информации).
Сжатие данных не может быть большим некоторого теоретического предела. Для формального определения этого предела рассматриваем любое информационное сообщение длины n как последовательность независимых, одинаково распределенных д.с.в. Xi или как выборки длины n значений одной д.с.в. X.
Доказано, что среднее количество бит, приходящихся на одно кодируемое значение д.с.в., не может быть меньшим, чем энтропия этой д.с.в., т.е.  для любой д.с.в. X и любого ее кода.
для любой д.с.в. X и любого ее кода.
Кроме того, доказано утверждение о том, что существует такое кодирование (Шеннона-Фэно), что  .
.
Примечание: функция L(X) возвращает длину сообщения, кодирующего заданное значение X; мат. Ожидание ML(X) - это средняя длина сообщения, кодирующего X. Можно формально определить L(X) через две функции L(X)=len(code(X)), где code(X) каждому значению X ставит в соответствие некоторый битовый код, причем, взаимно однозначно, а len возвращает длину в битах для любого конкретного кода.
Основная теорема о кодировании при отсутствии помех: с ростом длины сообщения при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения.
Подобное кодирование практически не реализуемо из-за того, что с ростом длины сообщения трудоемкость построения этого кода становится недопустимо большой. Кроме того, такое кодирование делает невозможным отправку сообщения по частям, что необходимо для непрерывных процессов передачи данных. Дополнительным недостатком этого способа кодирования является необходимость отправки или хранения собственно полученного кода вместе с его исходной длиной, что снижает эффект от сжатия. На практике для повышения степени сжатия используют метод блокирования: по выбранному значению можно выбрать такое 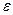 , что если разбить все сообщение на блоки длиной s (всего будет n/s блоков), то кодированием Шеннона-Фэно таких блоков, рассматриваемых как единицы сообщения, можно сделать среднее количество бит на единицу сообщения большим энтропии менее, чем на
, что если разбить все сообщение на блоки длиной s (всего будет n/s блоков), то кодированием Шеннона-Фэно таких блоков, рассматриваемых как единицы сообщения, можно сделать среднее количество бит на единицу сообщения большим энтропии менее, чем на 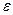 .
.
Пример. Пусть д.с.в. Xi независимы, одинаково распределены и могут принимать только два значения  и
и  при i от 1 до n. Тогда
при i от 1 до n. Тогда

Минимальное кодирование здесь - это коды 0 и 1 с длиной 1 бит каждый. При таком кодировании количество бит в среднем на единицу сообщения равно 1. Разобьем сообщение на блоки длины 2. Закон распределения вероятностей и кодирование для 2-мерной д.с.в.
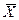
| ||||
| p | 9/16 | 3/16 | 3/16 | 1/16 |
| code(X) | ||||
| L(X) |
Тогда при таком минимальном кодировании количество бит в среднем на единицу сообщения будет уже 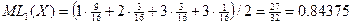 , т.е. меньше, чем для неблочного кодирования.
, т.е. меньше, чем для неблочного кодирования.
Все изложенное ранее подразумевало, что рассматриваемые д.с.в. кодируются только двумя значениями (обычно 0 и 1). Пусть д.с.в. кодируются m значениями. Тогда для д.с.в. 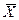 и любого ее кодирования верно, что
и любого ее кодирования верно, что  и
и  .
.
Кроме того, существует кодирование такое, что  и
и  , где n=dim(X).
, где n=dim(X).
Метод Шеннона-Фэно состоит в следующем, значения д.с.в. располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй - 1.
Для предшествующего примера получим
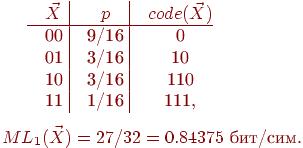
Пример: Закодируем с помощью метода Шеннона-Фэно фразу «Иванов Иван Иванович»
1. Вычисляем количество символов в сообщении (без учета пробелов) и частоту каждого символа.
L=18.
| И | В | А | Н | О | Ч |

2. Упорядочиваем символы по частоте появления в тексте по убыванию: В – И – А – Н – О – Ч.
3. Последовательно делим таблицу на две части с приблизительно равными частотами, к коду первой части добавляют 0, а к коду второй - 1.
| Символ | Частота | 1 шаг | 2 шаг | 3 шаг | Результат |
| В | |||||
| И | |||||
| А | |||||
| Н | |||||
| О | |||||
| Ч |
 - средняя длина кода
- средняя длина кода

Задание: Закодировать свою фамилию, имя отчество с помощью метода Шеннона-Фэно. Вычислить среднюю длину кода. Вычислить энтропию исходного текста.
Поиск по сайту: