Алгоритм Витерби

1. Инициализация. Номер яруса t = 0. Метрика нулевого узла приравнивается нулю, за этим узлом закрепляется «пустой» путь.

2. Для ярусов с номерами t= 1 ,…,L для каждого из узлов на ярусе выполняются следующие вычисления:

a. Находим метрику каждого из путей и ведущих в узел, как сумму метрик предшествующих узлов и ребер, связывающих узлы-предшественники с данным узлом.

b. Находим путь с минимальной метрикой и эту метрику приписываем данному узлу.

c. Путь, ведущий в узел, вычисляется дописыванием к пути, ведущему в выбранный предшествующий узел, информационного символа, соответствующего переходу из узла-предшественника в данный узел.

3. Путь, соответствующий единственному узлу на ярусе L, выдается получателю как результат декодирования.

Пути, сходящиеся в одном узле решетки, называют конкурирующими, а выбранный из их числа наилучший путь называют выжившим. Алгоритм Витерби на каждом ярусе решетки из каждого узла решетки «смотрит назад» на узлы предыдущего яруса. Находитметрики конкурирующих путей и выбирает путь с наименьшей метрикой. В результате, к последнему ярусу, выживает единственный путь, обладающий минимальной метрикой из всех возможных путей в решетке. На рисунке 10 приведен пример работы декодера Витерби в ДСК. Рассматривается усеченный код (7,5), решетка которого показана на рисунке.16.

Реализация алгоритма Витерби

Описание, приведенное в предыдущем разделе, иллюстрирует основную идею алгоритма Витерби. При практической реализации возникает ряд проблем, самые важные проблемы мы обсудим в данном разделе. К их числу мы относим:

- начало работы декодера;

- декодирование бесконечных последовательностей;

- организация памяти для хранения метрик путей;

- организация памяти для хранения выживших путей.

Из приведенной на рисунке 15 решетчатой диаграммы видно, что, пока номер яруса не превысил кодового ограничения кода v, структура решетки отличается от структуры решетки на остальных ярусах. Эта нерегулярность усложняет как программную, так и аппаратную реализацию декодирования.

Эта проблема имеет очень простое решение. Предположим, что декодирование производится по критерию минимальной метрики. В начале работы декодера всем состояниям, кроме нулевого, приписываются одинаковые и достаточно большие значения метрик. Нулевому узлу приписывается нулевая метрика. Далее выполняются точно такие же действия, как при декодировании на ярусах с номерами большими v. Нетрудно убедиться, что при таком назначении начальных метрик на ярусе с номером v декодер получит правильные значения метрик всех узлов. «Несуществующие» пути решетки будут отвергнуты декодером, поскольку их метрики будут больше метрик путей, исходящих из нулевого узла.

Применение алгоритма Витерби для декодирования бесконечных последовательностей.

Из описания алгоритма следует, что окончательное решение выдается декодеру только после обработки всей принятой выходной последовательности канала.

Понятно, что, если длина усечения кода велика или если используется неусеченный сверточный код, алгоритм не может быть использован из-за ограничений на задержку декодирования и сложность реализации.

Рисунок 16 - Пример декодирования в ДСК по алгоритму Витерби

Начало работы декодера.

Введем параметр T, представляющий собой максимальную задержку декодирования в числе информационных символов. Величина T существенно превышает кодовое ограничение кода v. На ярусе с номером T память путей декодера будет заполнена информационными последовательностями, соответствующими 2^v узлам решетки. Эти последовательности различны, но их число существенно меньше числа 2^T различных последовательностей длины T. На предыдущих шагах декодирования производилось сравнение метрик конкурирующих путей, и отбрасывались пути с худшими значениями метрик. Если величина T достаточно велика, то среди путей, начавшихся T ярусов назад, сохранилась лишь небольшая доля путей, и все они имеют достаточно хорошие значения метрик. Наиболее вероятна ситуация, когда на ярусе с номером 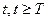, все пути имеют одинаковый бит, соответствующий ярусу с номером . Этот бит можно выдать получателю, стереть из памяти путей, произвести сдвиг всех путей в регистрах памяти на одну ячейку и тем самым освободить место для очередного информационного символа. В принципе, при сильном шуме в канале, возможно, что старшие биты в ячейках памяти путей различны. На этот случай нужно разработать стратегию формирования решений об информационных символах. На практике применяют одну из следующих стратегий:

- выбрать путь с наилучшей метрикой и выдать первый символ этого пути;

- подсчитать количество путей с различными значениями первого символа и принять решение по большинству;

- выдавать получателю первый символ одного и того же пути.

Нетрудно упорядочить эти стратегии по надежности и по сложности реализации, но можно заранее сказать, что при больших T разница между ними невелика. В практических схемах считается, что достаточно выбрать величину. Приблизительно в 5 - 6 раз больше длины кодового ограничения кода.

Вычисление и хранение метрик путей

Основная область применения декодера Витерби – каналы с мягкими решениями, т.е. каналы, в которых на значения входе кодера – вещественные числа. Для дальнейшей обработки они должны быть представлены в цифровой форме. От точности представления зависит сложность аналого-цифрового преобразования, сложность устройств, выполняющих арифметические операции над метриками ребер и путей, объем памяти для хранения метрик. В 70-е годы, когда разрабатывались первые реализации декодера Витерби, было принято считать, что для представления метрик символов достаточно 3 бит. По мере развития микроэлектроники ограничения на сложность арифметических устройств становились менее жесткими. Тем не менее, увеличение точности свыше 8 бит (для каналов с двоичным входным алфавитом) действительно не имеет смысла.

Итак, будем считать, что метрика одного символа записана в виде 1 байта. Сколько бит нужно для представления метрик путей? Если длина пути N составляет символов канала, то максимальное значение метрики путей может достигнуть величины N2⁸ и для хранения такой метрик нужно отвести (8+log₂N) двоичных ячеек памяти. При память любого объема неизбежно переполнится. В решении этой проблемы определяющую роль играет следующее наблюдение. Пусть v - кодовое ограничение кода, n - число кодовых символов, соответствующих ребру μ₀, - максимально значение метрики символа. Тогда разница между максимально и минимальной метрикой путей, выживших на данном ярусе, не превышает величины vnμ₀. Этот факт следует из того, что для любого узла решетки существует путь, ведущий в этот узел и отличающийся от пути с наименьшей метрикой не больше чем в символах. Если на некотором ярусе из всех значений метрик вычесть минимальное, это не повлияет на выбор путей в будущем, и, значит, вероятность ошибки декодирования не изменится. Эта операция (ее называют нормализациейметрик) может выполняться на каждом ярусе или один раз после обработки нескольких ярусов. В результате число бит для хранения метрик каждого пути приблизительно равно (8+log₂vn) и при реальных значения параметров кодера не превышает 16 бит.

Организация памяти для хранения путей. Каждый из выживших путей записывается в виде двоичной последовательности длины T. Заметим, что декодер Витерби, обрабатывая очередной узел решетчатой диаграммы, вычисляет новый путь, ведущий в данный узел, но не может занести его в ту же ячейку памяти, в которой хранился предыдущий путь. Дело в том, что предыдущий путь может понадобиться при обработке других узлов текущего яруса. Значит, нужно хранить два массива путей: «старые» и «новые». После обработки очередного яруса массивы меняются названиями. Таким образом, объем памяти для хранения путей составляет 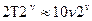. Именно эта память на практике определяет основные затраты на реализацию декодера. Существует альтернативный вариант реализации декодера, проигрывающий по скорости работы, но требующий вдвое меньше памяти для хранения путей. Этот вариант называют декодированием с возвращениями(back-trace decoder). Декодер с возвращениями на каждом ярусе работы после обработки узла заносит в память один бит, указывающий, какой из двух конкурирующих путей выбран.

Для выработки решения и выдачи получателю декодер, используя «обратный кодер» из текущего узла двигается назад по решетке и вычисляет путь в данный узел. Первый бит пути выдается получателю.

Поиск по сайту: