 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Методы эффективного кодирования при известной статистике сообщений
Метод Шеннона—Фано. Код Шеннона—Фано строится следующим образом: все имеющиеся К букв располагаются в один столбик в порядке убывания вероятностей. Затем эти буквы разбиваются на две группы: верхнюю и нижнюю так, чтобы суммарные вероятности этих групп были по возможности ближе друг к другу. Для букв верхней группы в качестве первого символа кодового слова используется «1», а для нижней—«0». Далее каждую из двух полученных групп нужно разделить на две части по возможности с близкими суммарными вероятностями; в качестве второго символа кодового слова используется «1» или «0» в зависимости от принадлежности букв верхней или нижней подгруппе и т. д. Данный процесс повторяется до тех пор, пока не приходим к группам, каждая из которых содержит по одной-единственной букве.
Пример 2. Пусть даны восемь сообщений (букв), имеющих следующие вероятности: 0,2; 0.2; 0,15; 0,13; 0,12; 0.10; 0,07; 0,03. Построение кода Шеннона—Фано дано в таблице 3.
Таблица 3- Построение кода Шеннона-Фано
| № сообщения | Вероятность появления сообщения | Деление сообщений на группы | Код Шеннона-Фано |
| 0,20 | 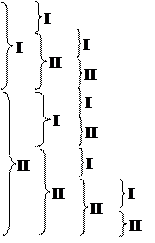
| ||
| 0,20 | |||
| 0,15 | |||
| 0,13 | |||
| 0,12 | |||
| 0,10 | |||
| 0,07 | |||
| 0,03 |
Если использовать равномерный код, то на кодирование данных восьми сообщений потребуется по три двоичных символа (бита); при использовании же кода Шеннона—Фано среднее число «0» и «1», приходящихся на одну букву сообщения, составит:
0,2•2+0,2•3+0,15•3+0,13•3+0,12•3+0,10•3+0,07•4+0,03•4=2,9.
Это меньше, чем при равномерном кодировании и не очень далеко от энтропии Н(А) =2,806 бит/сообщ.
Как следует из теоремы 2, особенно выгодно кодировать не отдельные буквы, а сразу целые блоки по несколько букв. Рассмотрим случай, когда имеются лишь две различные буквы а1 и а2, появляющиеся с вероятностью р(а1)=0,8 и р(а2)=0,2 соответственно. Тогда
Н(А) =-0,8log20,8—0,2log20,2=0,722 бит/буква.
Применяя метод Шеннона — Фано к исходному двухбуквенному алфавиту, получаем простейший код (Таблица 4).
Таблица 4 - Код двухбуквенного алфавита
| Буква | Вероятность | Код |
| a1 | 0,8 | |
| a2 | 0,2 |
Этот код требует для передачи каждой буквы одного двоичного символа (l =1), что на 38 % больше минимально возможного значения Н(А) =0,722 бит/буква.
Применим метод Шеннона — Фано к кодированию всевозможных двухбуквенных комбинаций (Таблица 5).
Таблица 5- Коды для двухбуквенных комбинаций
| Сообщение | Вероятность | Код |
| а1а1 | 0,64 | |
| а1а2 | 0,16 | |
| а2а1 | 0,16 | |
| а2а2 | 0,04 |
Средняя длина кодового слова здесь равна 1•0,64+2•0,16+3•0,2=1,56 бит.
Таким образом, на одну букву приходится 1,56/2=0,78 бит, что лишь на 8% больше значения 0,722. Еще лучший результат получим при кодировании трехбуквенных комбинаций (Таблица 6).
Таблица 6 - Коды для трехбуквенных комбинаций
| Сообщение | Вероятность | Код | Сообщение | Вероятность | Код |
| а1а1а1 | 0,512 | а1а2а2 | 0,032 | ||
| а1а1а2 | 0,128 | а2а1а2 | 0,032 | ||
| а1а2а1 | 0,128 | а2а2а1 | 0,032 | ||
| а2а1а1 | 0,128 | а2а2а2 | 0,008 |
Средняя длина кодового слова здесь равна 2,184 бит, т. е. на одну букву текста приходится в среднем 0,728 бит, что только на 0,83 % больше значения Н(А) =0,722 бит/букв.
Метод Хаффмена. Более выгодным, чем код Шеннона—Фано, является так называемый код Хаффмена. Пусть буквы (сообщения) входного алфавита А={a1,…,aк} имеют соответственно вероятности р1, р2,..., pк. Предположим, что буквы в алфавите расположены в порядке убывания их вероятностей (если данное условие не выполняется, то всегда нетрудно расположить буквы в порядке убывания их вероятностей. Это и будет первым шагом алгоритма Хаффмена), т.е. p1>=p2>=рк-1>=Рк. Тогда алгоритм кодирования Хаффмена состоит в следующем:
1) Два самых маловероятных сообщения объединяем в одно сообщение b, которое имеет вероятность, равную сумме вероятностей сообщений ak-1, ak, т.е. pk-1+pk. В результате получим сообщения а1, а2,..., aк-2, b, вероятности которых р1, p2, …, рк-2, pк-1+pк. Эти сообщения вновь располагаем в порядке убывания вероятностей.
2) Берем два сообщения, имеющие наименьшие вероятности, объединяем их в одно и вычисляем их в общую вероятность.
3) Повторяем шаги 1 и 2 до тех пор, пока не получим единственное сообщение, вероятность которого равна 1.
4) Проводя линии, объединяющие сообщения и образующие последовательные подмножества, получаем дерево, в котором отдельные сообщения являются концевыми узлами. Соответствующие им кодовые слова можно построить, приписывая ветви, которые идут вниз, «0», а вверх—«1».
Так как в процессе кодирования сообщениям сопоставляются только концевые узлы, полученный код является префиксным и всегда однозначно декодируем.
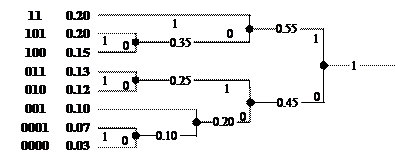
Построение кода Хаффмена для сообщений, появляющихся с вероятностями 0,2; 0,2; 0,15; 0,13; 0,12; 0,1; 0,07; 0,03, изображено на рисунке 2.
 | |||
|
Как видно из рисунка, он совпадает с кодом Шеннона—Фано, рассмотренным выше. Следовательно, по экономичности коды Шеннона—Фано и Хаффмена в данном конкретном случае одинаковы. Это еще раз подтверждает, что код Шеннона—Фано достаточно хорош. Однако в общем случае код Хаффмена экономичнее кода Шеннона—Фано.
Рассмотрим равномерное по выходу кодирование. Показанные выше методы кодирования являются оптимальными в том смысле, что эти методы кодирования позволяют затратить в среднем наименьшее число символов «0» и «1» на одно сообщение. Однако и метод Хаффмена, и метод Шеннона—Фано обладает следующими существенными недостатками:
1) если произойдет случайная ошибка, то она распространяется на все последующие сообщения, т.е. возникает так называемая ошибка синхронизации;
2) при декодировании, особенно при возникновении ошибки синхронизации, нужно использовать все передаваемые сообщения. Это потребует при передаче больших массивов информации огромной памяти.
Перечисленными выше недостатками не страдают так называемые равномерные коды. Эти коды используют для кодирования каждого сообщения одно и то же число символов «0» и «1», поэтому, если где-то произойдет ошибка, то она будет локализована именно в этом сообщении и на другие сообщения не распространяется. Опишем метод равномерного по выходу кодирования на примере, когда буквы входного алфавита А={а1, а2} появляется независимо с вероятностями р, q=1-p, причем р<1/2.
Предположим, что при кодировании допускается хотя и малая, но отличная от нуля вероятность ошибки. Рассмотрим множество An всех блоков длины п. Число таких блоков 2n Пусть n>0 и Tn - это подмножество блоков из Ап таких, что для них выполнено неравенство
|
где k—число букв a1 в блоке длины n; ε >0.
По закону больших чисел вероятность появления блока, принадлежащего Тn, больше или равна 1-pq/(nε2). При n→∞ эта вероятность стремится к единице.
Кодирование построим следующим образом. Рассмотрим множество блоков из «0» и «1», число которых равно числу элементов в Tn (число элементов в Tn обозначим Nт). Каждой последовательности из Tn сопоставляется свое кодовое слово, а всем последовательностям, не принадлежащим Tn, ставится в соответствие одно и то же выбранное заранее кодовое слово. Ясно, что при таком кодировании все сообщения из Tn будут воспроизводиться правильно, а при появлении сообщения, не принадлежащего Tn, будет происходить ошибка, которая, как видим, может быть сделана сколь угодно малой.
Среднее число символов «0» и «1», приходящихся на одну букву алфавита А, при этом кодировании равно (logNT)/n. Эта величина эквивалентна величине l, определяемой (5). Можно показать, что при n величина (logNT)/n стремится к H(A), т. е. основная теорема К. Шеннона справедлива и при описанном выше кодировании.
При p=0,11 для передачи сообщения из букв потребуется n=0,499 символов «0» и «1», что примерно в 2 раза меньше, чем n, при этом вероятность ошибки с ростом n стремится к нулю.
Рассмотренные выше методы кодирования источников нашли свое применение в основном в факсимильной связи.
Поиск по сайту: