Представление сверточного кода порождающими многочленами

Схема кодера двоичного сверточного кода в общем виде представлена на рисунок 7. Кодер содержит k двоичных регистров сдвига длин m₁,…,m_k. Входами регистров сдвига являются информационные символы. Выходы ячеек регистров соединены с сумматорами по модулю 2. Всего сумматоров n.

Рисунок 7 - Общая структурная схема кодера сверточного кода со скоростью k/n

На каждом такте работы кодера на его вход поступает блок k из информационных символов. Эти символы и символы, хранящиеся в данный момент в регистрах кодера, поступают на входы тех сумматоров, которые подключены к соответствующим ячейкам. Результаты сложения по модулю два поступают на выход схемы. После этого в каждом из регистров происходит сдвиг, новые информационные символы записываются в первые ячейки, а содержимое остальных ячеек сдвигается на один разряд.Содержимое 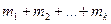ячеек регистров сдвига в каждый конкретный момент времени называется текущим состоянием кодера. Предположим, что в начальный момент времени кодер находится в некотором заранее известном состоянии. Примем для определенности это начальное состояние нулевым.

Рассмотрим процесс кодирования полубесконечнойинформационной последовательности.

Выходы сумматоров на каждом такте работы называются кодовыми символамисверточного кода. Полубесконечная последовательность кодовых символов называется кодовым словомсверточного кода. Множество всевозможных кодовых слов образует сверточный код.На каждом такте работы кодера k информационного символа используются для формирования n кодовых символов.

(1)

Отношение называется скоростью сверточного кода. Примеры кодеров сверточных кодов приведены на рисунке 8. Суммарная длина регистров сверточного кодера называется длиной кодового ограничения кода, а максимальная длина регистров называется задержкой кодера. Для кодов со скоростью память и кодовое ограничение совпадают.

Рисунок 8 - Примеры сверточных кодеров

Рассматриваемые схемы кодеров сверточных кодов полностью описываются связями ячеек регистров сдвига с выходными сумматорами. Существует несколько общепринятых форм представления этих связей. Начнем с кодов со скоростью 1/n. Связи каждого из n сумматоров с ячейками одного регистра длины записываются в виде двоичного вектора , . Ноль означает отсутствие связи, единица - наличие. Векторы g_i называют порождающими. В таблицах кодов порождающие векторы приводят в восьмеричной форме. Например, генератор будет записан как (125). Другие примеры показаны на рисунке 8 Порождающие векторы записывают также в виде полиномов формальной переменной D. Например, порождающие полиномы кодера, показанного на рисунке 8а, имеют вид

(2)

Эту совокупность полиномов можно также записать в виде матричного порождающего полинома

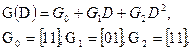(3)

Полиномиальное и матричное полиномиальное представление кодера удобно тем, что оно позволяет записать процесс кодирования в виде умножения и полиномов формальной переменной D. Предположим, что на вход кодера подается информационная последовательность . Эта последовательность может быть записана в виде полинома

(4)

Нетрудно убедиться в том, что на выходах сумматоров будут наблюдаться кодовые последовательности

(5)

Матричная запись имеет вид

(6)

Следовательно, на выходе кодера будет сформировано кодовое слово

.

В этом примере был рассмотрен код со скоростью 1/2. В случае кода со скоростью k/n схема кодера содержит k регистров сдвига. Обозначим через m максимальную длину регистра. Связи ячеек, имеющих одинаковый номер I с n выходными сумматорами, по-прежнему описываются матрицами , однако, поскольку таких ячеек теперь, размерность каждой из матриц будет равна k*n Кодер будет описан порождающим полиномом

(7)

Входная последовательность кодера будет представлена векторным полиномом

(8)

в котором подпоследовательности , имеют размерность 1*k. Кодирование представляется как умножение полиномов

(9)

Пример сверточного кода со скоростью 2/3 приведен на рисунке 8б.

Порождающая матрица сверточного кода. Из описания кодера или из формулы (9) непосредственно следует, что сверточный код является линейным. Это означает, что множество кодовых слов образует линейное пространство полубесконечных двоичных последовательностей.

Удобной формой представления блоковых линейных кодов является описание с помощью порождающей матрицы кода, строками которой, как известно, служат базисные векторы кода.

Хотя размерность пространства кодовых слов сверточного кода бесконечна, его регулярная структура позволяет в явном виде указать базис пространства и выписать порождающую матрицу сверточного кода. Рассмотрим сначала коды со скоростью 1/n. Заметим, что информационные последовательности вида

(10)

образуют в совокупности базис линейного пространства входных последовательностей кодера, поскольку любая информационная последовательность может быть представлена в виде линейной комбинации u_i, Каждой линейной комбинации информационных последовательностей u_i соответствует кодовая последовательность, равная линейной комбинации кодовых слов, соответствующих u_i. Отсюда следует, что кодовые слова, соответствующие этим информационным последовательностям, образуют базис в пространстве кодовых слов. Из (1) следует, что порождающая матрица сверточного кода может быть записана в виде:

(11)

где через 0 обозначена нулевая матрица размерности 1*n. В случае кодов со скоростью k/n формула (1.11) для порождающей матрицы сверточного кода также верна, но размерность составляющих подматриц будет k*n.

Поиск по сайту: