Декодирование сверточных кодов по максимуму правдоподобия. Алгоритм Витерби

Сверточные коды часто используются как внутренние коды в каскадных схемах кодирования. От эффективности их декодирования в большой степени зависит надежность системы в целом. Поэтому для их декодирования необходимо использовать трудоемкое, но оптимальное в смысле вероятности ошибки правило – декодирование по максимуму правдоподобия. Решающим преимуществом сверточных кодов перед блоковыми кодами является возможность применения весьма эффективной процедуры декодирования по максимуму правдоподобия – алгоритма Витерби. Данная лабораторная работа посвящена изучению алгоритма Витерби, способов его практической реализации и анализу его эффективности изучению алгоритма Витерби, способов его практической реализации и анализу его эффективности.

Декодирование по максимуму правдоподобия

Рассмотрим сначала блоковый код словами которого являются последовательности некоторого дискретного алфавита. Обозначим через Y множество символов, наблюдаемых на выходе канала. Это множество может быть дискретным или непрерывным. Для определенности вначале мы будем считать алфавит дискретным.

Предположим, что для передачи некоторого сообщения с номером использовано кодовое слово X_m и в результате передачи по каналу принята последовательность Y. Задача декодера состоит в принятии решения о том, какое из кодовых слов было передано M Правило декодирования задается разбиением множества выходных последовательностей канала на непересекающиеся подмножества такие, что при появлении на выходе канала последовательности принимается решение в пользу кодового слова. Множества называют решающими областями R, m.Формирование решающих областей определяется критерием принятия решений, который в свою очередь зависит от критерия качества системы связи. Для многих задач удовлетворительным критерием качества можно считать вероятность ошибки декодирования. Для блоковых кодов эта вероятность определяется как средняя по всем кодовым словам вероятность принять решение в пользу кодового слова при условии, что передавалось кодовое слов. Известно, что при равновероятных кодовых словах минимальная вероятность ошибки достигается при декодировании по критериюмаксимального правдоподобия (МП). Правило формирования решающих областей при этом имеет вид

(12)

где представляет собой условную вероятность появления на выходе канала последовательности y при передаче последовательности x. По определению, для заданной выходной последовательности y декодер МП принимает решение в пользу того кодового слова, для которого максимальна условная вероятность появления y на выходе канала. Вероятность называют функцией правдоподобия кодового слова x m.

Декодирование по МП требует точного описания модели канала, т.е. правила вычисления вероятностей p(y|x). Канал называют стационарным, если вероятности p(y|x) не зависят от положения последовательностей на оси времени, т.е. однозначно определяются конкретными значениями символов, образующих последовательности x и y. Канал называется каналом без памяти, если для всех n для любой пары последовательностей x =(x1…xn), y =(y1…yn) имеет место равенство:

(13)

Стационарный дискретный канал без памяти называется дискретнымпостоянным каналом(ДПК). Такой канал описывается переходными вероятностями {p(y|x), xÎX, yÎY}.

Вычислять функцию правдоподобия по формуле (3) не всегда удобно, поскольку для этого необходимо выполнять умножения. Вместо p(y|x) можно вычислять логарифмическую функцию правдоподобия

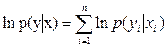(14)

Рассмотрим частный случай двоичного симметричного канала (ДСК), который представляет ДПК с двоичными алфавитами X=Y={0,1} и с переходными вероятностями: P(y=0|x=1)=p(y=1|x=0)=p, p(y=0|x=0)=p(y=1|x=1)=q=1-p

Такую модель называют двоичным симметричным каналом (ДСК). Для ДСК формула (1.14) принимает вид

(15)

где, d n(x,y) обозначает расстояние Хэмминга между последовательностями x и y.

Параметр p представляет собой переходную вероятность ДСК. Можно всегда предполагать что, p <1/2. Из формулы (5) следует, что для ДСК декодирование по МП эквивалентно декодированию по минимуму расстояния Хэмминга.

Другой важный случай – полунепрерывный канал с двоичным входом и гауссовским шумом. Входные символы выбираются из алфавита

X={-1,+1}.Условные распределения вероятностей значений на выходе канала имеют вид:

(16)

где через E обозначена энергия элементарного сигнала, а N0 /2 - дисперсия y,обусловленная действием в канале шума со спектральной плотностью мощности N 0/2. При передаче по каналу без памяти последовательности x длины n получим:

(17)

Таким образом, декодирование по МП эквивалентно поиску кодового слова x, для которого минимально евклидово расстояние

(18)

между последовательностью y и «сигнальной последовательностью»

Декодирование может быть выполнено еще проще, если принять во внимание, что

(19)

В правой части только вычитаемое зависит от конкретного кодового слова. Поэтому для декодирования по МП достаточно найти кодовое слово, для которого максимально скалярное произведение

(20)

Итак, для декодирования по МП необходимо по принятой последовательности y для каждого кодового слова вычислить его «метрику». В случае канала без памяти эта метрика является аддитивной, т.е. может быть вычислена как сумма метрик отдельных символов кодового слова. В зависимости от конкретной ситуации, необходимо найти кодовое слово с минимальной метрикой (как в ДСК) либо с максимальной метрикой (как в гауссовском канале). В дальнейшем для определенности будем считать, что задача декодера – найти путь с минимальной метрикой.

Поиск по сайту: