 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Методы эффективного кодирования при неизвестной статистике сообщений
Коды, экономичные одновременно для некоторого класса источников, называют универсальными кодами. Сформулируем постановку задачи универсального кодирования источников. Предположим, что алфавит состоит из двух букв a1 и a2, появляющихся независимо с вероятностями p, q=1- p. Однако величина pзаранее неизвестна. Требуется построить код, для которого среднее число символов «0» и «1» на одну букву алфавита приближалось бы к H(A) при любом p, 0<= p <=1. Этот код строится так. Множество всех блоков длины n в алфавите A разбиваем на группы, которые имеют одинаковые вероятности при любом р. Таких групп будет ровно n+1. В нулевой группе отсутствует буква a2, она состоит из единственного блока а1а1... а1, вероятность появления которого рn.
Первая группа состоит из всех блоков длины n, содержащих одну букву а2. Эта группа состоит из Сп1=п блоков, вероятность каждого из которых равна рn-1 q. Группа с номером k состоит из всех блоков длины п, содержащих k букв a2. Эта группа содержит п блоков, вероятность каждого из которых рn-k <qk.
Универсальный код для k -й группы состоит из двух частей: префикса и суффикса. Префикс содержит log2(n +1) двоичных знаков. Префикс указывает, к какой группе сообщений принадлежит кодируемый блок, суффикс содержит log Cn k двоичных символов и указывает номер блока в группе. Построенный таким образом код будет однозначно дешифруем. На приемном конце первоначально по log(n +1) элементам кода определяют, к какой группе принадлежит переданное сообщение, а затем по следующим log Cn k элементам определяют, какое именно сообщение передавалось.
Код 1 в таблице 7 построен описанным выше способом. Здесь выделены штриховой линией префиксы. Этот метод кодирования называется комбинаторным.
Префикс каждой из групп при комбинаторном кодировании содержит ровно log(n +1) символов «0» и «1». Еще большего эффекта можно достичь, если префикс кодировать неравномерным кодом (Рисунок 1). Код 2 в таблице 7 построен именно этим методом. Универсальные методы кодирования хороши не только тем, что они экономичны для любого распределения вероятностей, но и достаточно просто реализуются. Для универсального кодирования на передающем и приемном концах не обязательно знать таблицу, которая определяет кодирование.
Код каждого блока вычисляется по мере поступления на кодирующее устройство букв а1 и а2. На приемном конце также можно декодировать, не прибегая к таблицам. При этом число операций на кодирование и декодирование блока длины п не превосходит п3.
Таблица 7 - Кодирование при неизвестной статистике сообщений

Из приведенного выше описания метода кодирования видно, наиболее трудоемкой частью кодирования является нахождение суффикса. Опишем алгоритм нахождения суффикса. Пусть в блоке А длины п буква а1 встречается на местах i1, i2, …, ir, тогда суффиксом для А назовем число N(A), вычисляемое по правилу:
 (9)
(9)
Очевидно, что блоки с разными наборами (i1, …, ir) получают разные номера. При этом максимальное значение номера равно
 (10)
(10)
Таким образом, двоичная запись номера (суффикса) должна иметь длину | log Cnr |.
Для нахождения N(A) воспользуемся таблицей биноминальных коэффициентов (треугольником Паскаля):
Элементы этой таблицы вычисляются по мере надобности либо размещаются в памяти кодирующего устройства.
Приведем фрагмент этой таблицы, в которой на пересечении i-й строки и j-го столбца стоит  .
.
Пример 3. Пусть n =8, A=a2a1a1a2a1a1a2a1 тогда r =5; i1 =2, i2 =3, i3 =5, i4 =6, i5 =8.
Тогда номер блока N(A) =С11+С22+С43+С54+С75. Слагаемые в N(А) находим, используя таблицу дополнительных коэффициентов. Они выделены жирным шрифтом. Таким образом, N (А) =1+1+4+5+21=32 или в двоичной записи N(А) =100000.
Декодирование производится с помощью этой же таблицы.
Пример 4. Пусть нам известно, что длина передаваемого блока равна 8, и что в блоке пять букв а1 (количество букв в блоке находим по префиксу). Находим максимальное число в 5-м столбце, не превосходящее 32, это 21=С58-1, следовательно, i5=8, находим разность 32—21=11. Находим далее максимальное число 4-го столбца, не превосходящее 11. Это 5=C46-1 т. е. i4 =6. Аналогично находим i3 =5, i2 =3, i1 =2. Следовательно, декодированное сообщение имеет вид
A=a2a1a1a2a1a1a2a1, т.е. совпадает с переданным.
Рассмотренные кодирование и декодирование достаточно просто осуществляются с помощью специализированных вычислительных средств.
Метод Хаффмена
Одним из часто используемых методов кодирования является так называемый метод Хаффмена. Данный метод кодирования, позволяющий значительно сжимать информацию и построенный на основе двоичных кодирующих деревьев был предложен Д. А. Хаффменом в 1952 году задолго до появления современного цифрового компьютера. Метод обладает высокой эффективностью, он и его многочисленные адаптивные версии лидируют среди методов, используемых в алгоритмах кодирования.
Пусть сообщения входного алфавита А = {а1, а2, …, аk} имеют соответственно вероятности их появления р1, р2,..., рk.
Тогда алгоритм кодирования Хаффмена состоит в следующем.
1) Сообщения располагаются в столбец в порядке убывания вероятности их появления.
2) Два самых маловероятных сообщения ak-1, и аk объединяем в одно сообщение b, которое имеет вероятность, равную сумме вероятностей сообщений ak-1, аk, т. е. pk-1+pk. В результате получим сообщения a1, a2, …, ak-2, b, вероятности которых p1, p2, …, pk-2, (pk-1+pk). Полученные сообщения вновь располагаем в порядке убывания вероятностей.
3) Повторяем шаги 1 и 2 до тех пор, пока не получим единственное сообщение, вероятность которого равна 1.
4) Проводя линии, объединяющие сообщения и образующие последовательные подмножества, получаем дерево, в котором отдельные сообщения являются концевыми узлами. Соответствующие им кодовые комбинации можно определить, приписывая левым ветвям объединения символ «1», а правым - «0». Впрочем, понятия «левые» и «правые» ветви в данном случае относительны.
Так как в процессе кодирования сообщениям сопоставляются только кон-
цевые узлы, полученный код (код Хаффмена) является префиксным и, следовательно, всегда однозначно декодируемым.
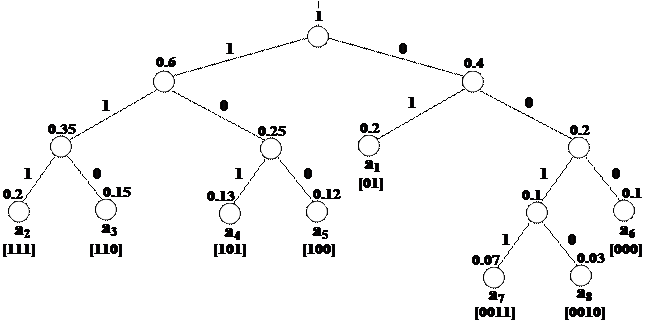
Построение кода Хаффмена для восьми сообщений, появляющихся с вероятностями 0.2; 0.2; 0.15; 0.13; 0.12; 0.1; 0.07; 0.03, иллюстрируется таблицей 8 и рисунком 5.
Таблица 8 - Кодирование методом Хаффмена
| Сообщение | Вероятность | Вспомогательные столбцы | ||||||||||
| a1 | 0.20 | 0.20 | 0.20 | 0.25 | 0.35 | 0.40 | 0.60 | |||||
| a2 | 0.20 | 0.20 | 0.20 | 0.20 | 0.25 | 0.35 | 0.40 | |||||
| a3 | 0.15 | 0.15 | 0.20 | 0.20 | 0.20 | 0.25 | ||||||
| a4 | 0.13 | 0.13 | 0.15 | 0.20 | 0.20 | |||||||
| a5 | 0.12 | 0.12 | 0.13 | 0.15 | ||||||||
| a6 | 0.10 | 0.10 | 0.12 | |||||||||
| a7 | 0.07 | 0.10 | ||||||||||
| a8 | 0.03 | |||||||||||
Из точки, соответствующей сумме всех вероятностей (в данном случае она равна 1), направляются две ветви. Ветви с большей вероятностью присваивается единица, с меньшей - нуль. Продолжая последовательно разветвлять дерево, доходим до вероятности каждого символа (Рисунок 3).
 | |||
|
Из таблицы 9 видно, что полученный код является неравномерным, причем сообщению с максимальной вероятностью появления соответствует минимальная длина кодовой комбинации (2 бита), а сообщению с минимальной
вероятностью - максимальная (4 бита).
Таблица 9 - Полученный код
| Вероятность появления сообщения | Структура кодовой комбинации | Длительность кодовой комбинации | |
| a1 | 0.20 | 2 бита | |
| a2 | 0.20 | 3 бита | |
| a3 | 0.15 | 3 бита | |
| a4 | 0.13 | 3 бита | |
| a5 | 0.12 | 3 бита | |
| a6 | 0.10 | 3 бита | |
| a7 | 0.07 | 4 бита | |
| a8 | 0.03 | 4 бита |
Пусть переданная последовательность сообщений а1, а2, а3, а4, а8 отображается двоичной последовательностью
| 0010… | (11) |
Рассмотрим влияние одиночной ошибки во втором разряде принятой кодовой последовательности на результат декодирования. При этом получим
| 0010... | (12) |
Полученная последовательность расшифровывается следующим образом
| a7, a2, a1, a1, a8 | (13) |
Из (12) видно, что искажение даже одного двоичного элемента (01) может привести к появлению ошибок в нескольких сообщениях (треку ошибок). Это является существенным недостатком рассмотренного метода кодирования.
Среднее число двоичных символов l на одно сообщение алфавита объемом К, для неравномерных двоичных кодов, определяется выражением
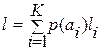 (14)
(14)
Эффективность неравномерных кодов оценивается следующими параметрами:
1) коэффициентом статистического сжатия, который характеризует уменьшение числа двоичных символов на знак при применении методов эффективного кодирования по сравнению с применением равномерного кода:
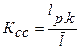 (15)
(15)
где lp.k - средняя длина кодовой комбинации при равномерном кодировании;
2) коэффициентом относительной эффективности, который показывает степень близости средней длины кодовой комбинации к теоретически возможному пределу Н(А):
 (16)
(16)
Поиск по сайту: