 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кодовое дерево сверточного кода и решетчатая диаграмма
Вернемся к коду (5,7), кодер которого показан на рис.1.8а. Считаем, что начальное состояние кодера было нулевым. Это состояние и все предыдущее мы будем отображать в виде узлов дерева. Возможные переходы из состояния в состояние соответствуют ребрам дерева. Каждому такому ребру соответствует некоторый блок из n =2 кодовых символов. Несколько начальных ярусов дерева, соответствующего коду (5,7), показано на рисунке 9. Это дерево называют кодовым. В связи с такой графической интерпретацией сверточного кода параметр n называют длиной ребра кода.
По кодовому дереву легко определить кодовое слово, соответствующее заданной информационной последовательности. На рисунке 9 движение вверх соответствует информационному символу 0, движение вниз - символу 1. Например, информационной последовательности 010110… соответствует кодовое слово 00111000. Обращает на себя внимание то, что число узлов дерева быстро растет от яруса к ярусу. В то же время, каждому узлу соответствует некоторое состояние кодера. Число различных состояний кода со скоростью 1/ n и с длиной кодового ограничения m в точности равно 2m. Следовательно, начиная с яруса с номером m +1, найдутся узлы соответствующие одинаковым состояниям. Поддеревья, начинающиеся в этих узлах, полностью идентичны. Чтобы сделать графическое представление кода более компактным, имеет смысл объединить узлы, соответствующие одинаковым состояниям и отображать их в виде одного узла.
Полученный таким образом граф называют решетчатой диаграммой сверточного кода. Решетчатая диаграмм кода (5,7) приведена на рисунке 1.10. В общем случае кода со скоростью 1/ n и кодовым ограничением на ярусах с номерами 
располагается 2t узлов, и из каждого исходит q =2 ребра. На ярусах с номерами 
число узлов равно 2m, в каждый узел входит 2 ребра и из каждого узла исходит 2 ребра. В случае кода со скоростью k/n и кодовым ограничением v максимальное число состояний равно 2v, число ребер, исходящих из каждого, узла равно 2k. По заданной информационной последовательности легко проследить кодовое слово. Поступление на вход кодера информационного символа 0 соответствует переходу в то из двух доступных из данного узла состояний, номер которого меньше. Поступление единицы приводит к переходу в состояние с большим номером. На рисунке 1.10 видно, что в первом случае мы двигаемся по решетке "вниз", во втором - "вверх". Представление кода решетчатой диаграммой чрезвычайно удобно для анализа декодирования сверточных кодов. Для изучения характеристик сверточных кодов удобно представление кодера в виде конечного автомата. Для кода (5,7) конечный автомат показан на рисунке 11. Конечный автомат описывается графом, узлы которого соответствуют состояниям кодера, а ребра - переходам из состояния в состояние. Видно, что из каждого состояния выходят ровно два ребра, соответствующие двум возможным значениям входных символов. Каждому ребру приписаны кодовые символы, порождаемы кодером при данном переходе.
Рисунок 9- Кодовое дерево кода (5,7)
Рисунок 10- Решетчатая диаграмма кода (5,7)
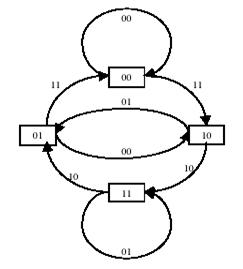
Рисунок 11- Конечный автомат, описывающий работу кодера кода (5,7)
Поиск по сайту: