АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Правило Лопиталя

Читайте также:
  1. Висновки моделі Солоу, Золоте правило нагромадження, роль технічного погресу в економічному зростанні.
  2. Данный принцип представляет собой правило, в соответствии с которым арбитражный суд исследует доказательства и фиксирует полученную устным путем информацию в письменной форме.
  3. Как правило, что нибудь да обязательно идет наперекосяк. Но иногда
  4. Кредитно-денежная политика по «правилам». Монетарное правило.
  5. Модель равновесия экономического роста Р. Солоу. «Золотое правило» накопления и дилемма государственной экономической политики регулирования экономического роста.
  6. Модель равновесного экономического роста Р. Солоу. «Золотое правило» накопления и дилемма государственной экономической политики регулирования экономического роста.
  7. Модель Солоу и «золотое правило накопления».
  8. Модель Солоу. Золоте правило нагромадження капіталу.
  9. Монетаризм. Денежное (монетарное) правило
  10. Монетаризм. Основное ур-ие монетаризма. Стабильн скорости обращ Д в монетаристской модели. Адаптивные ожидания и долгосрочн крив Филипса. Денежн правило.
  11. Монетаризм. Основное уравнение монетаризма. Денежное правило
  12. Общее правило признания доходов от реализации

Отчёт по теме

«Предел функции»

Теоремы о пределе:

Т-1 Функция не может иметь более одного предела.

Т-2 Для любого натурального показателя m и любого коэффициента k справедливо соотношение

Т-3 Если , , то

а) предел суммы равен сумме пределов

б) предел произведения равен произведению пределов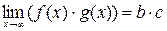

в) предел частного равен частному от пределов

г) постоянный множитель можно вынести за знак предела

Первый замечательный предел

Второй замечательный предел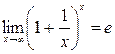

Следствие из второго замечательного предела

Бесконечно малые и бесконечно большие величины

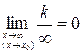
Правило Лопиталя

Если , то

1. Если нужно найти предел функции, которая представляет собой отношение двух многочленов, при этом X стремится к бесконечности, то главную роль играют только старшие степени этих многочленов. Т. е. при одинаковых показателях старшей степени предел равен отношению коэффициентов при этих степенях. Если степень многочлена в числителе больше, чем в знаменателе, то такой предел равен бесконечности. Если же показатель степени выше в знаменателе, то предел равен нулю.

2. В случаях, когда X стремится к нулю, главную роль играют слагаемые с самыми маленькими степенями икса.

3. Если при подстановке предельного значения аргумента в функцию получаются неопределённости вида ноль делить на ноль; ноль умножить на бесконечность; бесконечность делить на бесконечность, то можно использовать правило Лопиталя для нахождения значений таких пределов. Оно заключается в том, что предел отношения двух функций равен пределу отношения производных этих функций, если такие производные существуют.

4. Если в числителе или знаменателе дроби под знаком предела стоит разность квадратных корней от некоторых выражений, то самым удобным способом нахождения такого предела является умножение числителя и знаменателя на сопряжённую сумму корней.


Критерий оценки:

Каждое задание I уровня знаний – 0,5 балла

II уровня знаний – 1 балл

III уровня знаний – 5 баллов


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)