Основные теоремы кодирования

Кодирование информации

Основные понятия

Выше упоминались теоремы Шеннона о кодировании сообщений. Интуитивно понятно, что кодирование – это операция преобразования информации в форму, требуемую для последующей обработки (передачи по каналу связи, хранения в памяти вычислительной системы, использования для принятия решения и т.д.). Также понятно, что при построении любой информационной системы обойтись без кодирования невозможно: любое представление информации подразумевает использование каких-нибудь кодов. Поэтому далее подробно разберем теоретические основы кодирования информации.

Пусть A – произвольный алфавит. Элементы алфавита A называют буквами (или символами), а конечные последовательности, составленные из букв, – словами в A. При этом считается, что в любом алфавите существует пустое слово, не содержащее букв.

Слово α ₁ называют началом (префиксом) слова α, если существует слово α ₂, такое, что α = α ₁ α ₂; при этом слово α ₁ называют собственным началом слова α, если α ₂ – не пустое слово. Длина слова – это число букв в слове (пустое слово имеет длину 0). Запись α ₁ α ₂ обозначает соединение (конкатенацию) слов α ₁ и α ₂. Слово α ₂ называют окончанием (суффиксом) слова α, если существует слово α ₁, такое, что α = α ₁ α ₂; при этом слово α ₂ называют собственным окончанием слова α, если α ₁ – не пустое слово. Пустое слово по определению считается началом и окончанием любого слова α.

Рассмотрим алфавит B = {0, 1, …, D – 1}, где D ≥ 2, и произвольное множество C. Произвольное отображение множества C в множество слов в алфавите B называют D -ичным кодированием множества C (при D = 2 кодирование будет двоичным). Обратное отображение называют декодированием. Приведем примеры кодирований.

1. Кодирование множества натуральных чисел, при котором числу n = 0 ставится в соответствие слово e (0) = 0, а числу n ≥ 1 двоичное слово

e (n) = b ₁ b ₂ … b_{l ( n )}

наименьшей длины, удовлетворяющее условию

.

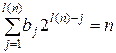Очевидно, что b ₁ = 1, 2 ^{l ( n ) – 1} ≤ n < 2 ^{l ( n )} и, следовательно

l (n) = [log n ] + 1 = ]log(n + 1)[,

где [ x ] и ] x [ обозначает соответственно наибольшее целое число, не превосходящее x, и наименьшее целое число, превосходящее x. Слово e (n) называют двоичной записью числа n, а данное кодирование – представление чисел в двоичной системе счисления. Данное кодирование является взаимно однозначным, поскольку при n ₁ ≠ n ₂ слова e (n ₁) и e (n ₂) различны. В таблице 5.1 приведено представление первых 16 натуральных чисел в двоичной системе счисления.

Таблица 5.1

Кодирование e (n)

2. Кодирование первых 2 ^k натуральных чисел, при котором каждому числу n (0 ≤ n < 2 ^k) ставится в соответствие слово

e_k (n) = 0 ^{k – l ( n )} e (n),

где запись 0 ^{k – l ( n )} обозначает слово, состоящее из k – l (n) нулей, e (n) – представление числа n в двоичной системе счисления, рассмотренное выше. Данное кодирование для первых 16 натуральных чисел (k = 4) приведено в таблице 5.2.

Таблица 5.2

Кодирование e_k (n)

Пусть A = { a_i, i = 1, 2, …} – конечный или счетный алфавит, буквы которого занумерованы натуральными числами. В этом случае кодирование букв алфавита A можно задать последовательностью D -ичных слов V = { v_i, i = 1, 2, …}, где v_i есть образ буквы a_i. Такие последовательности слов (из множества V) называют кодами (алфавита А). Если задан код V алфавита А, то кодирование слов, при котором каждому слову a_{i 1} a_{i 2}… a_ik ставится в соответствие слово v_{i 1} v_{i 2}… v_ik, называют побуквенным кодированием.

При переходе от взаимно однозначного кодирования букв алфавита к побуквенному кодированию слов в алфавите свойство взаимной однозначности может не сохраниться. Например, кодирование e (n) не сохраняет данное свойство, а кодирование e_k (n) его сохраняет. Свойство взаимной однозначности сохраняют разделимые коды. Код V = { v_i, i = 1, 2, …} называют разделимым, если из каждого равенства вида

v_{i 1} v_{i 2}… v_ik = v_{j 1} v_{j 2}… v_jl

следует, что l = k и v_{i 1} = v_{j 1}, v_{i 2} = v_{j 2}, …, v_ik = v_jl. Разделимые коды называют также однозначно декодируемыми кодами.

К классу разделимых кодов принадлежат префиксные коды. Код V = { v_i, i = 1, 2, …} называют префиксным, если никакое слово v_k не является началом (префиксом) никакого слова v_l, l ≠ k. Если каждое слово префиксного кода заменить наименьшим его началом, которое не является началом других кодовых слов, то полученный код также будет префиксным. Такую операцию называют усечением префиксного кода.

Для произвольного кода V, состоящего из различных слов, можно построить кодовое дерево. Это ориентированный граф, не содержащий циклов, в котором вершина β ₁ соединена с вершиной β ₂ ребром, направленным от β ₁ к β ₂, тогда и только тогда, когда β ₂ = β ₁ b, где b Î B = {0, 1, …, D – 1}, D ≥ 2. Для префиксных кодов (и только для них) множество кодовых слов совпадает с множеством концевых вершин (вершин, из которых не исходят ребра) кодового дерева.

Основные теоремы кодирования

Свойства кодов, полезные для их практического применения, определяются основными теоремами кодирования.

Теорема 5.1. Неравенство Крафта. Для существования однозначно декодируемого (разделимого) кода, содержащего N кодовых слов в множестве {0, 1, D – 1} с длинами n ₁, n ₂, …, n_N, необходимо и достаточно, чтобы выполнялось неравенство

.

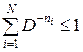Доказательство. Представим, что имеется кодовое дерево для префиксного кода. Корень кодового дерева образует уровень 0, вершины, связанные с корнем, – уровень 1 и т.д. Возможное количество вершин на k -м уровне обозначим как D^k. Каждая вершина k -го уровня порождает точно D^{n – k} вершин n -го уровня.

Далее для простоты упорядочим длины кодовых слов:

n ₁ ≤ n ₂ ≤…≤ n_N = n.

Очевидно, что кодовое слово длины k запрещает в точности D^{n – k} возможных концевых вершин (вершин последнего уровня). Тогда все кодовые слова префиксного кода запрещают 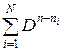концевых вершин. Так как общее число концевых вершин равно Dⁿ, то справедливо неравенство

,

из которого следует, что

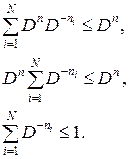
Таким образом, неравенство Крафта доказано.

В результате доказательства теоремы 5.1 делается вывод о том, что существуют хотя бы префиксные коды, которые являются однозначно декодируемыми кодами, с длинами кодовых слов n ₁, n ₂, …, n_N, удовлетворяющими неравенству Крафта. Следующая теорема, называемая утверждением Мак-Миллана, обобщает данный вывод на все однозначно декодируемые коды.

Теорема 5.2. Неравенство Мак-Миллана. Каждый однозначно декодируемый код удовлетворяет неравенству Крафта.

Доказательство. Возведем сумму 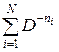в степень L:

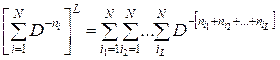. (5.1)

Пусть A_k – число комбинаций, содержащих L кодовых слов с суммарной длиной k. Тогда выражение (6.1) можно представить в виде

,

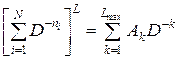где L _max – максимальная длина сообщения, содержащего L кодовых слов. Если код является однозначно декодируемым, то все последовательности из L кодовых слов суммарной длины k различны. Так как имеется всего D^k возможных последовательностей, то A_k ≤ D^k и тогда

Так как L – это число независимых кодовых слов, которые используются для построения всех возможных последовательностей длины, не превышающей L _max. Поэтому L ≤ L _max и 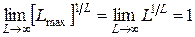. А из этого следует, что

.

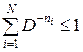Поскольку приведенные рассуждения справедливы для каждого однозначно декодируемого кода, а не только для префиксных кодов, то утверждение Мак-Миллана доказано.

Следующие теоремы связывают энтропию источника сообщений и среднюю длину кодового слова.

Теорема 5.3. Теорема кодирования источников I. Для любого дискретного источника без памяти X с конечным алфавитом и энтропией H (X) существует D -ичный префиксный код, в котором средняя длина кодового слова 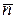удовлетворяет неравенству

. (5.2)

Доказательство. Прежде всего, поясним, что дискретный источник без памяти, описывается моделью, в которой не учитываются связи между символами сообщения. Теперь докажем левую часть неравенства (6.2):

.

Для этого используем определение энтропии и неравенство Крафта:

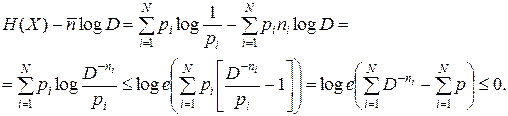
Для доказательства правой части неравенства (6.2) перепишем неравенство Крафта в следующем виде:

.

Затем выберем для каждого слагаемого такое наименьшее целое n_i, при котором

.

Так как неравенство Крафта при таком выборе сохраняется, то можно построить соответствующий префиксный код. Так как n_i – наименьшее целое, то для n_i – 1 справедливо

.

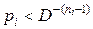Тогда

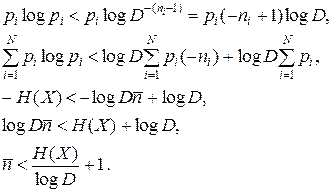
Таким образом, теорема кодирования источников I доказана. Она определяет, что средняя длина кодового слова не может быть меньше энтропии источника сообщений. Отметим, что при доказательстве теоремы использовались те же обозначения, что и при рассмотрении неравенства Крафта.

Теорема 5.4. Теорема кодирования источников II. Для блока длины L существует D -ичный префиксный код, в котором средняя длина кодового слова на один символ 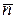удовлетворяет неравенству

,

где .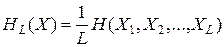

Доказательство. Здесь в качестве единиц сообщений рассматриваются блоки символов и H (X ₁, X ₂, …, X _L) – это энтропия источника сообщений, приходящаяся на блок из L символов. Для доказательства теоремы можно воспользоваться теоремой о кодировании источников I:

Теорема о кодировании источников II позволяет утверждать, что существуют такие способы кодирования для достаточно длинного сообщения, что средняя длина кодового слова может быть сделана сколь угодно близкой к величине 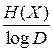. Действительно, при L ® ∞, H_L (X) ® H, где H – энтропия источника сообщений на один символ, справедливо неравенство

, (5.3)

где 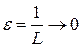. Это можно интерпретировать также следующим образом: для любого сколь угодно малого числа ε, существует метод кодирования блоков, содержащих символов, при котором для средней длины кодового слова на символ 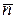выполняется неравенство (5.3).

Кроме того, так как минимально достижимой длиной кодового слова на символ является величина , то при D = 2 избыточность кода можно определить по формуле .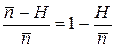

Поиск по сайту: