 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Оптимальное кодирование. Задача построения оптимального кода заключается в отыскании целых положительных чисел n1, n2, , nN
Задача построения оптимального кода заключается в отыскании целых положительных чисел n 1, n 2, …, nN, минимизирующих среднюю длину кодового слова при условии выполнения неравенства Крафта:
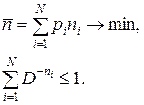
При построении кодов в случае алфавита A = { ai, i = 1, 2, …, N } с известным распределением вероятностей P = { pi, i = 1, 2, …, N } без ограничения общности можно считать, что буквы алфавита A занумерованы в порядке убывания их вероятностей, т.е. p 1 ≥ p 2 ≥ … ≥ pN. Кроме того, будем рассматривать только двоичные коды.
Известны два метода (Фано и Шеннона) построения кодов, близких к оптимальным. Метод Фано заключается в следующем. Упорядоченный в порядке убывания вероятностей список букв делится на две последовательные части так, чтобы суммы вероятностей входящих в них букв как можно меньше отличались друг от друга. Буквам из первой части приписывается символ 0, а буквам из второй части – символ 1. Далее точно также поступают с каждой из полученных частей, если она содержит, по крайней мере, две буквы. Процесс продолжается до тех пор, пока весь список не разобьется на части, содержащие по одной букве. Каждой букве ставится в соответствие последовательность символов, приписанных в результате этого процесса данной букве. Легко видеть, что полученный код является префиксным.
Метод Шеннона применим лишь в том случае, когда все вероятности положительны. Он состоит в том, что букве ai, имеющей вероятность pi > 0, ставится в соответствие последовательность из ni = ]log(1/ pi)[ первых после дробной точки цифр разложения числа  в бесконечную дробь (для a 1 полагаем, что q 1 = 0). Поскольку при l > k (в силу того, что pl ≤ pk) nl ≥ nk и
в бесконечную дробь (для a 1 полагаем, что q 1 = 0). Поскольку при l > k (в силу того, что pl ≤ pk) nl ≥ nk и 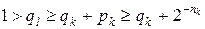 , то полученный таким образом код является префиксным. На основе полученного префиксного кода строится усеченный префиксный код, который и является результатом кодирования по методу Шеннона.
, то полученный таким образом код является префиксным. На основе полученного префиксного кода строится усеченный префиксный код, который и является результатом кодирования по методу Шеннона.
Пусть, например, имеется множество букв A = { a 1, a 2, a 3, a 4, a 5, a 6, a 7} с распределением вероятностей P = {0.2, 0.2, 0.19, 0.12, 0.11, 0.09, 0.09}. Выполним кодирование букв по методу Фано.
1. Разобьем список на две части, так чтобы суммы вероятностей, входящих в них букв как можно меньше отличались друг от друга:
A 1 = { a 1, a 2, a 3}, P 1 = {0.2, 0.2, 0.19};
A 2 = { a 4, a 5, a 6, a 7}, P 2 = {0.12, 0.11, 0.09, 0.09}.
2. Припишем буквам из первой части символ 0, а буквам второй части символ 1:
A 1 = { a 1/0, a 2/0, a 3/0};
A 2 = { a 4/1, a 5/1, a 6/1, a 7/1}.
3. Повторим последовательно указанные действия для каждой из частей по отдельности. В результате получим:
A 11 = { a 1/00};
A 121 = { a 2/010};
A 122 = { a 3/011};
A 211 = { a 4/100};
A 212 = { a 5/101};
A 221 = { a 6/110};
A 222 = { a 7/111}.
Кодовые слова, полученные в результате кодирования, приведены для каждой буквы справа от наклонной черты. При этом порядок индексов полученных однобуквенных списков показывает последовательность разбиения исходного списка групп на части.
Процесс кодирования по методу Фано удобно оформлять в виде таблицы. Для рассматриваемого примера он приведен в таблице 5.3.
Таблица 5.3
Кодирование по методу Фано
| a 1 | 0.20 | ||||
| a 2 | 0.20 | ||||
| a 3 | 0.19 | ||||
| a 4 | 0.12 | ||||
| a 5 | 0.11 | ||||
| a 6 | 0.09 | ||||
| a 7 | 0.09 |
Определим среднюю длину кодового слова:
 .
.
Теперь выполним кодирование по методу Шеннона. Процесс кодирование приведено в таблице 5.4.
Таблица 5.4
Кодирование по методу Шеннона
| ai | ni | qi | Код ai | Усеченный код ai |
| a 1 | ]2.321…[ = 3 | |||
| a 2 | ]2.321…[ = 3 | 0.2 | ||
| a 3 | ]2.395…[ = 3 | 0.4 | ||
| a 4 | ]3.058…[ = 4 | 0.59 | ||
| a 5 | ]3.183…[ = 4 | 0.71 | ||
| a 6 | ]3.472…[ = 4 | 0.82 | ||
| a 7 | ]3.472…[ = 4 | 0.91 |
Как и предыдущего случая найдем среднюю длину кодового слова:
 .
.
Как можно видеть результаты кодирования по методам Фано и Шеннона с точки зрения минимизации средней длины кода практически совпали. Поэтому часто эти методы рассматривают как один (в формулировке Фано) и называют методом Шеннона-Фано.
В 1952 г. Давид Хаффмен предложил метод оптимального префиксного кодирования для дискретных источников, который в отличие от методов Шеннона и Фано до сих пор применяется на практике. Д.Хаффмен доказал, что средняя длина кодового слова, полученная с помощью его метода, будет минимальна. Кодирование Хаффмена производится за три шага.
1. Упорядочение: буквы располагаются в порядке убывания их вероятностей.
2. Редукция: две буквы с наименьшими вероятностями объединяются в одну с суммарной вероятностью; список букв переупорядочивается в соответствии с шагом 1; процесс продолжается до тех пор, пока все буквы не будут объединены в одну. При этом можно добиться выравнивания длин кодовых слов с помощью следующей стратегии: если несколько букв имеют одинаковые вероятности, то объединяют те две из них, которые до этого имели наименьшее число объединений (правда на среднюю длину кода это не повлияет).
3. Кодирование: начиная с последнего объединения, последовательно приписываются одной компоненте составной буквы символ 0, а второй – символ 1; процесс продолжается до тех пор, пока все исходные буквы не будут закодированы.
Выполним кодирование по методу Хаффмена для множества, рассматривавшегося в примерах применения методов Фано и Шеннона.
1. Исходный список букв A = { a 1, a 2, a 3, a 4, a 5, a 6, a 7} уже упорядочен, так как P = {0.2, 0.2, 0.19, 0.12, 0.11, 0.09, 0.09}.
2. Объединим буквы a 6 и a 7 в одну букву a 1 с вероятностью 0.18 и переупорядочим список:
P 1 = {0.2, 0.2, 0.19, 0.18, 0.12, 0.11}, A 1 = { a 1, a 2, a 3, a 1, a 4, a 5}.
3. Повторим шаг 2 до тех пор, пока не останется одна буква в списке:
P 2 = {0.23, 0.2, 0.2, 0.19, 0.18}, A 2 = { a 2, a 1, a 2, a 3, a 1};
P 3 = {0.37, 0.23, 0.2, 0.2}, A 3 = { a 3, a 2, a 1, a 2};
P 4 = {0.4, 0.37, 0.23}, A 4 = { a 4, a 3, a 2};
P 5 = {0.6, 0.4}, A 5 = { a 5, a 4};
P 6 = {1}, A 6 = { a 6}.
4. Присвоим двоичные коды символам:
a 6: a 5 = 0, a 4 = 1;
a 5: a 3 = 00, a 2 = 01;
a 4: a 1 = 10, a 2 = 11;
a 3: a 3 = 000, a 1 = 001;
a 2: a 4 = 010, a 5 = 011;
a 1: a 6 = 0010, a 7 = 0011.
Таким образом, исходным буквам присвоены следующие двоичные коды: a 1 = 10, a 2 = 11, a 3 = 000, a 4 = 010, a 5 = 011, a 6 = 0010, a 7 = 0011, что дает среднюю длину кода  , меньшую, чем в случае кодирования Фано и Шеннона.
, меньшую, чем в случае кодирования Фано и Шеннона.
Определим избыточность полученных кодов. Для этого найдем энтропию источника сообщений:
 .
.
Тогда коды имеют следующую избыточность:
код Фано:  ;
;
код Шеннона: 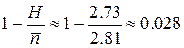 ;
;
код Хаффмена:  .
.
Таким образом, избыточность кода Хаффмена минимальна.
Для снижения избыточности, т.е. снижения средней длины кодового слова на один символ, можно воспользоваться блочным кодированием, обоснование которого дано в теореме кодирования источников II. В этом случае необходимо получить всевозможные группы букв заданной длины, найти вероятности групп, как вероятности совместного появления букв группы одновременно, и выполнить кодирование, рассматривая группы как символы нового алфавита.
Поиск по сайту: