Блочное двоичное кодирование

Вернемся к проблеме оптимального кодирования. Пока что наилучший результат (наименьшая избыточность) был получен при кодировании по методу Хаффмана - для русского алфавита избыточность оказалась менее 1 %. При этом указывалось, что код Хаффмана улучшить невозможно. На первый взгляд это противоречит первой теореме Шеннона, утверждающей, что всегда можно предложить способ кодирования, при котором избыточность будет сколь угодно малой величиной. На самом деле это противоречие возникло из-за того, что до сих пор мы ограничивали себя алфавитным кодированием. При алфавитном кодировании передаваемое сообщение представляет собой последовательность кодов отдельных знаков первичного алфавита. Однако возможны варианты кодирования, при которых кодовый знак относится сразу к нескольким буквам первичного алфавита (будем называть такую комбинацию блоком) или даже к целому слову первичного языка. Кодирование блоков понижает избыточность. В этом легко убедиться на простом примере.

Пусть имеется словарь некоторого языка, содержащий n=16000 слов (это, безусловно, более чем солидный словарный запас!). Поставим в соответствие каждому слову равномерный двоичный код. Очевидно, длина кода может быть найдена из соотношения K(A, 2)≥log₂n≥ 13,97 = 14. Следовательно, каждое слово кодируется комбинацией из 14 нулей и единиц - получатся своего рода двоичные иероглифы. Например, пусть слову "ИНФОРМАТИКА" соответствует код 10101011100110, слову "НАУКА" - 00000000000001, а слову "ИНТЕРЕСНАЯ" - 00100000000010; тогда последовательность:

очевидно, будет означать "ИНФОРМАТИКА ИНТЕРЕСНАЯ НАУКА". 76

Легко оценить, что при средней длине русского слова K^(r) =6,3 буквы (5,3 буквы + пробел между словами) средняя информация на знак первичного алфавита оказывается равной I^(A)=K(A,2)=14/6,3 = 2,222 бит, что более чем в 2 раза меньше, чем 5 бит при равномерном алфавитном кодировании. Для английского языка такой метод кодирования дает 2,545 бит на знак. Таким образом, кодирование слов оказывается более выгодным, чем алфавитное.

Еще более эффективным окажется кодирование в том случае, если сначала установить относительную частоту появления различных слов в текстах и затем использовать код Хаффмана. Подобные исследования провел в свое время Шеннон: по относительным частотам 8727 наиболее употребительных в английском языке слов он установил, что средняя информация на знак первичного алфавита оказывается равной 2,15 бит.

Вместо слов можно кодировать сочетания букв - блоки. В принципе блоки можно считать словами равной длины, не имеющими, однако, смыслового содержания. Удлиняя блоки и применяя код Хаффмана теоретически можно добиться того, что средняя информация на знак кода будет сколь угодно приближаться к L.

Пример 3.2.

Пусть первичный алфавит состоит из двух знаков а и b с вероятностями, соответственно, 0,75 и 0,25. Сравнить избыточность кода Хаффмана при алфавитном и блочном двухбуквенном кодировании.

При алфавитном кодировании:

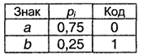
I(А) =0,811, К(А,2) = 1, Q(A,2) = 0,233

При блочном двухбуквенном кодировании (очевидно, p_ij=pi∙p_j):

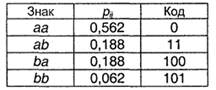
I(A) = 1,623 (в пересчете на 1 знак - 0,811), К(А,2) = 1,688 (в пересчете на знак - 0,844), Q(A,2) =0,040.

Таким образом, блочное кодирование обеспечивает построение более оптимального кода, чем алфавитное. При использовании блоков большей длины (трехбуквенных и более) избыточность стремится к 0 в полном соответствии с первой теоремой Шеннона.

Контрольные вопросы и задания

1. Приведите примеры обратимого и необратимого кодирования помимо рассмотренных в тексте.

2. В чем смысл первой теоремы Шеннона для кодирования?

3. Первичный алфавит содержит 8 знаков с вероятностями: "пробел" - 0,25; "?" - 0,18; "&" - 0,15; "*" - 0,12; "+" - 0,1; "%" - 0,08; "!" - 0,07 и "!" - 0,05. В соответствии с правилами, изложенными в п.3.2.1, предложите вариант неравномерного алфавитного двоичного кода с разделителем знаков, а также постройте коды Шеннона-Фано и Хаффмана; сравните их избыточности.

4. Постройте в виде блок-схемы последовательность действий устройства, производящего декодирование сообщения, коды которого удовлетворяют условию Фано. Реализуйте программно на каком-либо языке программирования.

5. Является ли кодирование по методу Шеннона-Фано и по методу Хаффмана однозначным? Докажите на примере алфавита А, описанного в п.3.2.1.

6. С помощью электронных таблиц проверьте правильность данных о средней длине кода К(А,2) для всех обсуждавшихся в п.3.2.1. примерах неравномерного алфавитного кодирования.

7. Продолжите пример 3.2, определив избыточность при трехбуквенном блочном кодировании.

8. Для алфавита, описанного в задаче 3, постройте вариант минимального кода Бодо.

9. Проверьте данные об избыточность кода Бодо для русского и английских языков, приведенных в п.3.2.2. Почему избыточность кода для русского языка меньше?

10. Почему в 1 байте содержится 8 бит?

11. Оцените, какое количество книг объемом 200 страниц может поместиться:

• (a) на дискете 1,44 Мб;
• (b) в ОЗУ компьютера 32 Мб?
• (c) на оптическом CD-диске емкостью 650 Мб?
• (d) на жестком магнитном диске винчестера емкостью 8,4 Гб?

12. Почему в компьютерных устройствах используется байтовое кодирование?

13. Что такое "лексикографический порядок кодов"? Чем он удобен?

14. Для цифр придумайте вариант байтового кодирования. Реализуйте процедуру кодирования программно (ввод - последовательность цифр; вывод - последовательность двоичных кодов в соответствии с разработанной кодовой таблицей).

15. Разработайте программу декодирования байтовых кодов из задачи 13.

16. Код Морзе для цифр следующий:

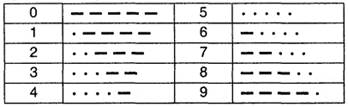
17. Считая алфавит цифр самостоятельным, а появление различных цифр равновероятным, найдите избыточность кода Морзе для цифрового алфавита.

В лексиконе "людоедки" Эллочки Щукиной из романа Ильфа и Петрова "12 стульев" было 17 словосочетаний ("Хо-хо!", "Ого!", "Блеск!", "Шутишь, парниша", "У вас вся спина белая" и пр.).

(a) Определите длину кода при равномерном словесном кодировании.

(b) Предложите вариант равномерного кодирования данного словарного запаса.

Поиск по сайту: