Цена кодирвания

Пусть заданы алфавит и вероятности появления букв в сообщении (p_i – вероятность появления буквы a_i). Не ограничивая общности, можно считать, что p_i+…+p_n=1 и 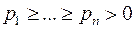(то есть можно сразу исключить буквы, которые не могут появиться в сообщении, и упорядочить буквы по убыванию вероятности их появления).

Для каждой (разделимой) схемы алфавитного кодирования математическое ожидание коэффициента увеличения длины сообщения при кодировании (обозначается ) определяется следующим образом:

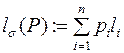, где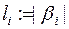

и называется средней ценой (или длиной) кодирования при распределении вероятностей P.

Пример

Для разделимой схемы А={a,b}, B={0,1}, 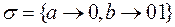при распределении вероятностей цена кодирования составляет 0.5*1+0.5*2=1.5, а при распределении вероятностей она равна 0.9*1+0.1*2=1.1.

Обозначим

Очевидно, что всегда существует разделимая схема , такая что . Такая схема называется схемой равномерного кодироваия. Следовательно, и достаточно учитывать только такие схемы, для которых 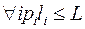, где l_i целое и 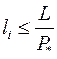. Таким образом, имеется лишь конечное число схем , для которых . Следовательно, существует схема , на которой инфимум достигается:

Алфавитное (разделимое) кодирование , для которого , называется кодированием с минимальной избыточностью, или оптимальным кодированием, для распределения вероятностей P.

Алгоритм Фано

Следующий рекурсивный алгоритм строит разделимую префиксную схему алфавитного кодирования, близкого к оптимальному.

Алгоритм 6.1. Построение кодирования, близкого к оптимальному

Вход: P: array [1..n] of real – массив вероятностей появления УКВ в сообщении, упорядоченный по невозрастанию; .

Выход: C: array [1..n, 1..L] of 0..1 – массив элементархых кодов.

Fano (1, n, 0) { вызов рекурсивной процедуры Fano }

Основная работа по построению элементарных кодов выполняется следующей рекурсивной процедурой Fano.

Вход: b – индекс начала обрабатываемой части массива P, е – индекс конца обрабатываемой части массива P, к – длина уже построенных кодов в обрабатываемой части массива С.

Выход: заполненный массив С.

if e > b then

k:=k+1 { место для очередного разряда в коде }

m:=Med (b, e) { деление массива на две части }

for I from b to e do

C [i,k]:= I > m { в первой части добавляем 0, во второй - 1 }

end for

Fano (b, m, k) { обработка первой части }

Fano (m+1, e, k) { обработка второй части }

end if

Функция Med находит медиану указанной части массива P [b..e], то есть определяет такой индекс m (), что сумма элементов P [b..m] наиболее близка к сумме элементов P [m+1..e].

Вход: b – индекс начала обрабатываемой части массива P, e – индекс концап обрабатываемой части массива P.

Выход: m – индекс медианы, то есть

S_b:= {сумма элементов первой части }

for i from b to e-1 do

S_b:=S_b+P[i] { вначале все, кроме последнего }

end for

S_e:=P[e] { сумма элементво второй части }

M:= e { начинаем искать медиану с конца }

repeat

d:=S_b-S_e { разность сумм первой и второй части }

m:=m-1 { сдвигаем границу медианы вниз }

S_b:=S_b-P[m];

S_e:=S_e+P[m]

until |S_b-S_e| d

return m

Обоснование

При каждом удлинении кодов в одной части коды удлиняются нулями, а в другой – единицами. Таким образом, коды одной части не могут быть префиксами другой. Удлинение кода заканчивается тогда и только тогда, когда длина части равна 1, то есть остается единственный код. Таким образом, схема по построению префиксная, а потому разделимая.

Пример

Коды, построенные алгоритмом Фано для заданного распределения (n=7).

Поиск по сайту: