АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Классификация ошибок

Читайте также:
  1. CASE - технология. Классификация программных средств.
  2. I. ЛИЗИНГОВЫЙ КРЕДИТ: ПОНЯТИЕ, ИСТОРИЯ РАЗВИТИЯ, ОСОБЕННОСТИ, КЛАССИФИКАЦИЯ
  3. I. Типичные договоры, основные обязанности и их классификация
  4. VII. Причины возникновения ошибок при передаче текста Нового Завета
  5. Акции, их классификация и особенности
  6. Аминокислоты – структурные единицы белка. Классификация аминокислот по структуре радикала. Заменимые и незаменимые аминокислоты. Значение для организма незаменимых аминокислот.
  7. Апластические анемии: этиология, патогенез, клиника, классификация, диагностика, принципы лечения.
  8. Ассортимент изделий из пластмасс. Классификация, основные виды и требования к изделиям из пластмасс.
  9. Ассортимент, классификация трикотажных изделий
  10. Безусловные рефлексы. Классификация
  11. Билет 2. Взаимодействие объектов хоз.деят-ти человека с ОС. Классификация загрязнений ОС.
  12. Бортовые отсосы. Кольцевые отсосы. Применение. Классификация. Конструирование

Ошибка в канале могут быть следующих типов:

Ø 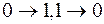- ошибка Тима замещения разряда;

Ø - ошибка типа выпадения разряда;

Ø - ошибка типа вставки разряда.

Канал характеризуется верхними оценками количества ошибок каждого типа, которые возможны при передаче через канал сообщения определенной длины. Общая характеристика ошибок канала (то есть их количество и типы) обозначается

Пример

Допустим, что имеется канал с характеристикой , то есть в канале возможна одна ошибка типа замещения разряда при передаче сообщения длины n. Рассмотрим следующее кодирование: F(a):=aaa (то есть каждый разряд в сообщении утраивается) и декодирование F-1(abc):=a+b+c>1 (то есть разряд восстанавливается методом «голосования»). Это кодирование кажется помехоустойчивым для данного канала, однако на самом деле это не так. Дело в том, что при передаче сообщения длины 3n возможно не более 3 ошибок типа замещения разряда, но места этих ошибок совершенно не обязательно распределены равномерно по всему сообщению. Ошибки замещения могут произойти в соседних разрядах, и метод голосования восстановит разряд неверно.

Возможность исправления всех ошибок

Пусть - множество слов, которые могут быть получены из слова s в результате всех возможных комбинаций допустимых в канале ошибок 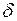, то есть 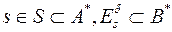. Если , то та конкретная последовательность ошибок, которая позволяет получить из слова s слово s’, обозначается 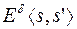. Если тип возможных ошибок в канале подразумевается, то индекс 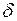не указывается.

ТЕОРЕМА чтобы существовало помехоустойчивое кодирование с исправлением всех ошибок, необходимо и достаточно, чтобы 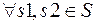, то есть неошходимо и достаточно, чтобы существовало разбиение множества B* на множества Bs (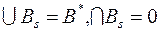), такое что .

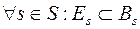Доказательство

Если кодирование помехоустойчивое, то очевидно, что . Обратно: по разбиению 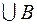, строится функция .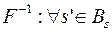

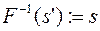Пример

Рассмотрим канал, в котором в любом передаваемом разряде происходит ошибка типа замещения с вероятностью P (0<p<1/2), причем замещения различных разрядов статистически независимы. Такой канал называется двоичным симметричным. В этом случае любое слово 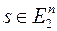может быть преобразовано в любое другое слово 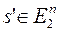замещениями разрядов. Таким образом, 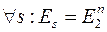, и исправить все ошибки в двоичном симметричном канале невозможно.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)