Разделимые схемы

Рассмотрим схему алфавитного кодирования и различные слова, составленные из элементарных кодов. Схема называется разделимой, если

,

То есть любое слово, составленное из элементарных кодов, единственным образом разлагается на элементарные коды. Алфавитное кодирование с разделимой схемой допускает декодирование.

Если таблица кодов содержит одинаковые элементарные коды, то есть если

где , то схема заведомо не является разделимой. Такие схемы далее не рассматриваются, то есть

Префиксные схемы

Схема называется префиксной, если элементарный код одной буквы не является префиксом элементарного кода другой буквы:

ТЕОРЕМА Префиксная схема является разделимой.

Доказательство

От противного. Пусть кодирование со схемой не является разделимым. Тогда существует такое слово , что

Поскольку , значит, , но это противоречит тому, что схема префиксная.

ЗАМЕЧАНИЕ

Свойство быть префиксной является достаточным, но не является необходимым для разделимости схемы.

Пример

Разделимая, но не префиксная схема: .

Неравенства Макмиллана

Чтобы схема алфавитного кодирования была разделимой, необходимо, чтобы длины элементарных кодов удовлетворяли определенному соотношению, известному как неравенство Макмиллана.

ТЕОРЕМА Если схема разделима, то

, где

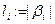
Доказательство

Обозначим . Рассмотрим n-ю степень левой части неравенства

.

Раскрывая скобки, имеем сумму

где i_1...i_n – различные наборы номеров элементарных кодов. Обозначим через количество входящих в эту сумму слагаемых вида 1/2^t, где t=l_i1+…+l_in. Для некоторых t может быть, что =0. Приводя подобные, имеем сумму

.

Каждому слагаемому вида ()^-1можно однозначно сопоставить код (слово в алфавите B) вида 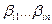. Это слово состоит из n элементарных кодов и имеет длину t.

Таким образом, 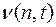- это число некоторых слов вида 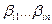, таких, что . В силу разделимости схемы , в противном случае заведомо существовали бы два одинаковых слова , допускающих различное разложение. Имеем

Следовательно, , и значит , откуда

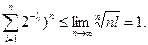
Неравенство Макмиллана является не только необходимым, но и в некотором смысле достаточным условием разделимости схемы алфавитного кодирования.

ТЕОРЕМА Если числа l₁…l_n удовлетворяет неравенству

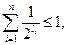
то существует разделимая схема алфавитного кодирования , где

Доказательство

Без ограничений общности можно считать, что . Разобьем множество {l₁,…,l_n} на классы эквивалентности по равенству {L₁,…,L_m}, m n.

Пусть

Тогда неравенство Макмиллана можно записать так:

Из этого неравенства следуют m неравенств для частичных сумм:

	(1)
	(2)
……….
	(m)

Рассмотрим слова длины в алфавите В. Поскольку , из этих слов можно выбрать различных слов длины . Исключим из дальнейшего рассмотрения все слова из В^*, начинающиеся со слов . Далее рассмотрим множество слов в алфавите В длиной и не начинающихся со слов . Таких слов будет . Но , значит, можно выбрать различных слов. Обозначим их . Исключим слова, начинающиеся с , из дальнейшего рассмотрения. И та далее, используя неравенства для частичных сумм, мы будем на i-м шаге выбирать слов длины , , причем эти слова не будут начинаться с тех слов, которые были выбраны раньше. В то же время длины этих слов все время растут (так как ), поэтому они не могут быть префиксами тех слов, которые выбраны раньше. Итак, в конце имеем набор из n слов , коды не являются префиксами друг друга, а значит, схема будет префиксной и, по теореме предыдущего подраздела, разделимой.

Пример

Азбука Морзе – это схема алфавитного кодирования

<A 01,B 1000,C 1010,D 100,E 0,F 0010,G 110,

H 0000,I 00,J 0111,K 101,L 0100,M 11,N 10,

O 1111,P 0110,Q 1101,R 010,S 000,T 1,U 001,

V 0001,W 011,X 1001,Y 1011,Z 1100>,

где по историческим и техническим причинам 0 называется точкой и обозначается знаком «.», а 1 называется тире и обозначается знаком «-». Имеем:

¼+1/16+1/16+1/8+½+1/16+1/8+1/16+¼+1/16+

1/8+1/16+1/4+1/4+1/8+1/16+1/16+1/8+1/8+

½+1/8+1/16+1/8+1/16+1/16+1/16 =

= 2/2 + 4/4 + 7/8 + 12/16 = 3+5/8 > 1.

Таким образом, неравенство Макмиллана для азбуки Морзе не выполнено, и эта схема не является разделимой. На самом деле в азбуке Морзе имеются дополнительные элементы – паузы между буквами (и словами), которые позволяют декодировать сообщения. Эти дополнительные элементы определены неформально, поэтому прием и передача сообщений с помощью азбуки Морзе, особенно с высокой скоростью, является некоторым искусством, а не простой технической процедурой.

Поиск по сайту: