Постановка задачи кодирования. Первая теорема Шеннона

Глава 3. Кодирование символьной информации

Теория кодирования информации является одним из разделов теоретической информатики. К основным задачам, решаемым в данном разделе, необходимо отнести следующие:

• разработка принципов наиболее экономичного кодирования информации;
• согласование параметров передаваемой информации с особенностями канала связи;
• разработка приемов, обеспечивающих надежность передачи информации по каналам связи, т.е. отсутствие потерь информации.

Две последние задачи связаны с процессами передачи информации - они будут рассмотрены в гл. 5. Первая же задача - кодирование информации - касается не только передачи, но и обработки, и хранения информации, т.е. охватывает широкий круг проблем; частным их решением будет представление информации в компьютере. С обсуждения этих вопросов и начнем освоение теории кодирования.

Постановка задачи кодирования. Первая теорема Шеннона

Как отмечалось при рассмотрении исходных понятий информатики, для представления дискретных сообщений используется некоторый алфавит. Однако однозначное соответствие между содержащейся в сообщении информацией и его алфавитом отсутствует.

В целом ряде практических приложений возникает необходимость перевода сообщения хода из одного алфавита к другому, причем, такое преобразование не должно приводить к потере информации.

Введем ряд с определений.

Будем считать, что источник представляет информацию в форме дискретного сообщения, используя для этого алфавит, который в дальнейшем условимся называть первичным. Далее это сообщение попадает в устройство, преобразующее и представляющее его в другом алфавите - этот алфавит назовем вторичным.

Код - (1) правило, описывающее соответствие знаков или их сочетаний первичного алфавита знакам или их сочетаниям вторичного алфавита.

(2) набор знаков вторичного алфавита, используемый для представления знаков или их сочетаний первичного алфавита.

Кодирование - перевод информации, представленной сообщением в первичном алфавите, в последовательность кодов.

Декодирование - операция, обратная кодированию, т.е. восстановление информации в первичном алфавите по полученной последовательности кодов.

Кодер - устройство, обеспечивающее выполнение операции кодирования.

Декодер - устройство, производящее декодирование.

Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечивает возврат к исходной информации без каких-либо ее потерь.

Примером обратимого кодирования является представление знаков в телеграфном коде и их восстановление после передачи. Примером кодирования необратимого может служить перевод с одного естественного языка на другой - обратный перевод, вообще говоря, не восстанавливает исходного текста. Безусловно, для практических задач, связанных со знаковым представлением информации, возможность восстановления информации по ее коду является необходимым условием применения кода, поэтому в дальнейшем изложении ограничим себя рассмотрением только обратимого кодирования.

Кодирование предшествует передаче и хранению информации. При этом, как указывалось ранее, хранение связано с фиксацией некоторого состояния носителя информации, а передача - с изменением состояния с течением времени (т.е. процессом). Эти состояния или сигналы будем называть элементарными сигналами -именно их совокупность и составляет вторичный алфавит.

Не обсуждая технических сторон передачи и хранения сообщения (т.е. того, каким образом фактически реализованы передача-прием последовательности сигналов или фиксация состояний), попробуем дать математическую постановку задачи кодирования.

Пусть первичный алфавит А состоит из N знаков со средней информацией на знак I^(A), а вторичный алфавит В- из М знаков со средней информацией на знак I^(В). Пусть также исходное сообщение, представленное в первичном алфавите, содержит п знаков, а закодированное сообщение - т знаков. Если исходное сообщение содержит I_st(A) информации, а закодированное - I_fin(B),то условие обратимости кодирования, т.е. неисчезновения информации при кодировании, очевидно, может быть записано следующим образом:

смысл которого в том, что операция обратимого кодирования может увеличить количество информации в сообщении, но не может его уменьшить. Однако каждая из величин в данном неравенстве может быть заменена произведением числа знаков на среднее информационное содержание знака, т.е.:

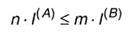
или

Отношение т/n, очевидно, характеризует среднее число знаков вторичного алфавита, которое приходится использовать для кодирования одного знака первичного алфавита - будем называть его длиной кода или длиной кодовой цепочки и обозначим К(А,В). Следовательно

Обычно N>M и I(А) > I(B), откуда К(А,В) > 1, т.е. один знак первичного алфавита представляется несколькими знаками вторичного. Поскольку способов построения кодов при фиксированных алфавитах А и Б существует множество, возникает проблема выбора (или построения) наилучшего варианта - будем называть его оптимальным кодом. Выгодность кода при передаче и хранении информации - это экономический фактор, так как более эффективный код позволяет затратить на передачу сообщения меньше энергии, а также времени и, соответственно, меньше занимать линию связи; при хранении используется меньше площади поверхности (объема) носителя. При этом следует сознавать, что выгодность кода не идентична временной выгодности всей цепочки кодирование-передача-декодирование; возможна ситуация, когда за использование эффективного кода при передаче придется расплачиваться тем, что операции кодирования и декодирования будут занимать больше времени и иных ресурсов (например, места в памяти технического устройства, если эти операции производятся с его помощью).

Как следует из β.1), минимально возможным значением средней длины кода будет:

Данное выражение следует воспринимать как соотношение оценочного характера, устанавливающее нижний предел длины кода, однако, из него неясно, в какой степени в реальных схемах кодирования возможно приближение К(А,В) к K^min(A,B). По этой причине для теории кодирования и теории связи важнейшее значение имеют две теоремы, доказанные Шенноном. Первая - ее мы сейчас рассмотрим - затрагивает ситуацию с кодированием при отсутствии помех, искажающих сообщение. Вторая теорема относится к реальным линиям связи с помехами и будет обсуждаться в гл. 5.

Первая теорема Шеннона, которая называется основной теоремой о кодировании при отсутствии помех, формулируется следующим образом:

При отсутствии помех всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак первичного алфавита, будет сколь угодно близко к отношению средних информации на знак первичного и вторичного алфавитов.

Приведенное утверждение является теоремой и, следовательно, должно доказываться. Мы опустим его, адресовав интересующихся именно доказательной стороной к книге А. М. Яглома и И. М. Яглома [49, с.212-217]. Для нас важно, что теорема открывает принципиальную возможность оптимального кодирования, т.е. построения кода со средней длиной К^min(А,В). Однако необходимо сознавать, что из самой теоремы никоим образом не следует, как такое кодирование осуществить практически - для этого должны привлекаться какие-то дополнительные соображения, что и станет предметом нашего последующего обсуждения.

Из (3.2) видно, что имеются два пути сокращения K^min(A,B):

• уменьшение числителя - это возможно, если при кодировании учесть различие частот появления разных знаков в сообщении, корреляции двухбуквенные, трехбуквенные и т.п. (в п.2.3. было показано, что I₀>I₁>I₂>…>I_∞);
• увеличение знаменателя - для этого необходимо применить такой способ кодирования, при котором появление знаков вторичного алфавита было бы равновероятным, т.е. I^(B)=log₂M.

В частной ситуации, рассмотренной подробно К. Шенноном, при кодировании сообщения в первичном алфавите учитывается различная вероятность появления знаков (то, что в п.2.3. мы назвали "первым приближением"), однако, их корреляции не отслеживаются - источники подобных сообщений называются источниками без памяти. Если при этом обеспечена равная вероятность появления знаков вторичного алфавита, то, как следует из β.2), для минимальной средней длины кода оказывается справедливым соотношение:

В качестве меры превышения К(А,В) над K^min(A, B) можно ввести относительную избыточность кода (Q(A,B):

Данная величина показывает, насколько операция кодирования увеличила длину исходного сообщения. Очевидно, Q(A,B) → 0 при К(А,В) → К^min(А,В). Следовательно, решение проблемы оптимизации кода состоит в нахождении таких схем кодирования, которые обеспечили бы приближение средней длины кода к значению K^min(AB),равному отношению средних информации на знак первичного и вторичного алфавитов. Легко показать, что чем меньше Q(A,B), тем I_fin(B) ближе к Ist(A)),т.е. возникает меньше информации, связанной с кодированием, более выгодным оказывается код и более эффективной операция кодирования.

Используя понятие избыточности кода, можно построить иную формулировку теоремы Шеннона:

При отсутствии помех всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.

Наиболее важной для практики оказывается ситуация, когда М = 2, т.е. для представления кодов в линии связи используется лишь два типа сигналов - технически это наиболее просто реализуемый вариант (например, существование напряжения в проводе (будем называть это импульсом) или его отсутствие (пауза); наличие или отсутствие отверстия на перфокарте или намагниченной области на дискете); подобное кодирование называется двоичным. Знаки двоичного алфавита принято обозначать "О" и "1", но нужно воспринимать их как буквы, а не цифры. Удобство двоичных кодов и в том, что при равных длительностях и вероятностях каждый элементарный сигнал (0 или 1) несет в себе 1 бит информации (log₂M = 1); тогда из β.3)

и первая теорема Шеннона получает следующую интерпретацию:

При отсутствии помех средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.

Применение формулы (3.4) для двоичных сообщений источника без памяти при кодировании знаками равной вероятности дает:

При декодировании двоичных сообщений возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) кодовых слов (групп элементарных сигналов), соответствующих отдельным знакам первичного алфавита. При этом приемное устройство фиксирует интенсивность и длительность сигналов, а также может соотносить некоторую последовательность сигналов с эталонной (таблицей кодов).

Возможны следующие особенности вторичного алфавита, используемого при кодировании:

• элементарные сигналы (0 и 1) могут иметь одинаковые длительности (τ₀=τ₁) или разные (τ₀≠τ₁);
• длина кода может быть одинаковой для всех знаков первичного алфавита (в этом случае код называется равномерным) или же коды разных знаков первичного алфавита могут иметь различную длину (неравномерный код);
• коды могут строиться для отдельного знака первичного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов).

Комбинации перечисленных особенностей определяют основу конкретного способа кодирования, однако, даже при одинаковой основе возможны различные варианты построения кодов, отличающихся своей эффективностью. Нашей ближайшей задачей будет рассмотрение различных схем кодирования для некоторых основ.

3.2. Способы построения двоичных кодов
3.2.1. Алфавитное неравномерное двоичное кодирование
сигналами равной длительности. Префиксные коды

Как следует из названия, в способах кодировании, относящихся к этой группе, знаки первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. О и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Длительности элементарных сигналов при этом одинаковы (τ₀=τ₁=τ). Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время /С(Д2)-т. Таким образом, задачу оптимизации неравномерного кодирования можно сформулировать следующим образом: построить такую схему кодирования, в которой суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей. За счет чего возможна такая оптимизация? Очевидно, суммарная длительность сообщения будет меньше, если применить следующий подход: тем знакам первичного алфавита, которые встречаются в сообщении чаще, присвоить меньшие по длине коды, а тем, относительная частота которых меньше - коды более длинные. Другими словами, коды знаков первичного алфавита, вероятность появления которых в сообщении выше, следует строить из возможно меньшего числа элементарных сигналов, а длинные коды использовать для знаков с малыми вероятностями.

Параллельно должна решаться проблема различимости кодов. Представим, что на выходе кодера получена следующая последовательность элементарных сигналов:

Каким образом она может быть декодирована? Если бы код был равномерным, приемное устройство просто отсчитывало бы заданное (фиксированное) число элементарных сигналов (например, 5, как в коде Бодо) и интерпретировало их в соответствии с кодовой таблицей. При использовании неравномерного кодирования возможны два подхода к обеспечению различимости кодов.

Первый состоит в использовании специальной комбинации элементарных сигналов, которая интерпретируется декодером как разделитель знаков. Второй - в применении префиксных кодов. Рассмотрим подробнее каждый из подходов.

Неравномерный код с разделителем

Условимся, что разделителем отдельных кодов букв будет последовательность 00 (признак конца знака), а разделителем слов-слов - 000 (признак конца слова - пробел). Довольно очевидными оказываются следующие правила построения кодов:

• код признака конца знака может быть включен в код буквы, поскольку не существует отдельно (т.е. кода всех букв будут заканчиваться 00);
• коды букв не должны содержать двух и более нулей подряд в середине (иначе они будут восприниматься как конец знака);
• код буквы (кроме пробела) всегда должен начинаться с 1;
• разделителю слов (000) всегда предшествует признак конца знака; при этом реализуется последовательность 00000 (т.е., если в конце кода встречается комбинация ...000 или ...0000, они не воспринимаются как разделитель слов); следовательно, коды букв могут оканчиваться на 0 или 00 (до признака конца знака).

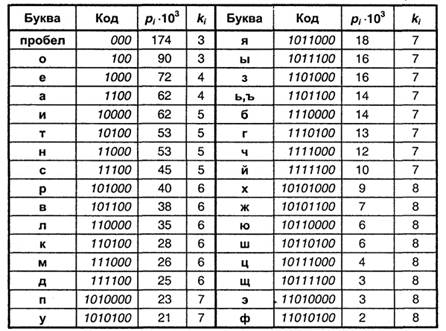
В соответствии с перечисленными правилами построим кодовую табл. 3.1 для букв русского алфавита, основываясь на приведенных ранее (табл. 2.1.) вероятностях появления отдельных букв.

Теперь по формуле (А.11) можно найти среднюю длину кода К(r,2) для данного способа кодирования:

Поскольку для русского языка, как указывалось в п.2.3., I^(r)₁ =4,356 бит, избыточность данного кода, согласно (3.5), составляет:

Q(r,2)=4,964/4,356-1≈0,14,

это означает, что при данном способе кодирования будет передаваться приблизительно на 14% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение К(е,2) =4,716, что при I^(e)₁ = 4,036 бит приводят к избыточности кода Q(e,2) =0,168.

Таблица 3.1

Рассмотрев один из вариантов двоичного неравномерного кодирования, попробуем найти ответы на следующие вопросы: возможно ли такое кодирование без использования разделителя знаков? Существует ли наиболее эффективный (оптимальный) способ неравномерного двоичного кодирования?

Суть первой проблемы состоит в нахождении такого варианта кодирования сообщения, при котором последующее выделение из него каждого отдельного знака (т.е. декодирование) оказывается однозначным без специальных указателей разделения знаков. Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию Фано):

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом⁸) какого-либо иного более длинного кода.

Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления с таблицей кодов всегда можно точно указать, где заканчивается один код и начинается другой.

Пример 3.1.

Пусть имеется следующая таблица префиксных кодов:

Требуется декодировать сообщение:

00100010000111010101110000110

Декодирование производится циклическим повторением следующих действий:

• (a) отрезать от текущего сообщения крайний левый символ, присоединить справа к рабочему кодовому слову;
• (b) сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (а);
• (c) декодировать рабочее кодовое слово, очистить его;
• (d) проверить, имеются ли еще знаки в сообщении; если "да", перейти к (а).

Применение данного алгоритма дает:

Доведя процедуру до конца, получим сообщение: "мама мыла раму".

Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных. Мы рассмотрим две схемы построения префиксных кодов.

Префиксный код Шеннона-Фано

Данный вариант кодирования был предложен в 1948-1949 гг. независимо Р. Фано и К. Шенноном и по этой причине назван по их именам. Рассмотрим схему на следующем примере: пусть имеется первичный алфавит А, состоящий из шести знаков a₁…a₆, с вероятностями появления в сообщении, соответственно, 0,3; 0,2; 0,2; 0,15; 0,1; 0,05. Расположим эти знаки в таблице в порядке убывания вероятностей (см. табл. 3.2). Разделим знаки на две группы таким образом, чтобы суммы вероятностей в каждой из них были бы приблизительно равными. В нашем примере в первую группу попадут а1 и а2 с суммой вероятностей 0,5 - им присвоим первый знак кода "О". Сумма вероятностей для остальных четырех знаков также 0,5; у них первый знак кода будет "1". Продолжим деление каждой из групп на подгруппы по этой же схеме, т.е. так, чтобы суммы вероятностей на каждом шаге в соседних подгруппах были бы возможно более близкими. В результате получаем:

Из процедуры построения кодов легко видеть, что они удовлетворяют условию Фано и, следовательно, код является префиксным. Средняя длина кода равна:

К(А,2) =0,3∙2 + 0,2∙2 + 0,2∙2 + 0,15∙3 + 0,1 ∙4 + 0,05∙4 = 2,45

I^(A)₁ = 2,390 бит. Подставляя указанные значения в (3.5), получаем избыточность кода Q(A,2) = 0,0249, т.е. около 2,5%. Однако, данный код нельзя считать оптимальным, поскольку вероятности появления 0 и 1 неодинаковы (0,35 и 0,65, соответственно). Применение изложенной схемы построения к русскому алфавиту дает избыточность кода 0,0147.

Префиксный ход Хаффмана

Способ оптимального префиксного двоичного кодирования был предложен Д. Хаффманом. Построение кодов Хаффмана мы рассмотрим на том же примере. Создадим новый вспомогательный алфавит А,, объединив два знака с наименьшими вероятностями (а₅ и а₆) и заменив их одним знаком (например, а⁽¹⁾; вероятность нового знака будет равна сумме вероятностей тех, что в него вошли, т.е.-0,15; остальные знаки исходного алфавита включим в новый без изменений; общее число знаков в новом алфавите, очевидно, будет на 1 меньше, чем в исходном. Аналогичным образом продолжим создавать новые алфавиты, пока в последнем не останется два знака; ясно, что количество таких шагов будет равно N - 2, где N - число знаков исходного алфавита (в нашем случае N = 6, следовательно, необходимо построить 4 вспомогательных алфавита). В промежуточных алфавитах каждый раз будем переупорядочивать знаки по убыванию вероятностей. Всю процедуру построения представим в виде таблицы:

Теперь в обратном направлении проведем процедуру кодирования. Двум знакам последнего алфавита присвоим коды 0 и 1 (которому какой - роли не играет; условимся, что верхний знак будет иметь код 0, а нижний - 1). В нашем примере знак а алфавита A(4), имеющий вероятность 0,6, получит код 0, а вероятностью 0,4 - код 1. В алфавите A знак а с -получает от а его вероятность 0,4 и код (1); коды знаков а и а, происходящие от знака а с вероятностью 0,6, будут уже двузначным: их первой цифрой станет код их "родителя" (т.е. 0), а вторая цифра - как условились - у верхнего 0, у нижнего - 1; таким образом, а будет иметь код 00, а а - код 01. Полностью процедура кодирования представлена в таблице, приведенной на с.70.

Из процедуры построения кодов вновь видно, что они удовлетворяют условию Фано и, следовательно, не требуют разделителя. Средняя длина кода, как и в предыдущем примере оказывается:

Избыточность снова оказывается равной Q(A2) = 0,0249, однако, вероятности 0 и 1 сблизились (0,47 и 0,53, соответственно). Более высокая эффективность кодов Хаффмана по сравнению с кодами Шеннона-Фано становится очевидной, если сравнить избыточности кодов для какого-либо естественного языка. Применение описанного метода для букв русского алфавита порождает коды, представленные в табл. 3.2. (для удобства сопоставления они приведены в формате табл. 3.1).

Таблица 3.2

Средняя длина кода оказывается равной K(r, 2)= 4,395; избыточность кода Q(r,2) = 0,0090, т.е. не превышает 1 %, что заметно меньше избыточности кода Шеннона-Фано (см. выше).

Код Хаффмана важен в теоретическом отношении, поскольку можно доказать, что он является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана (см. [49, с.209-211]).

Таким образом, можно заключить, что существует способ построения оптимального неравномерного алфавитного кода. Не следует думать, что он представляет число теоретический интерес. Метод Хаффмана и его модификация - метод адаптивного кодирования (динамическое кодирование Хаффмана) - нашли широчайшее применение в программах-архиваторах, программах резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах.

3.2.2. Равномерное алфавитное двоичное кодирование.
Байтовый код

В этом случае двоичный код первичного алфавита строится цепочками равной длины, т.е. со всеми знаками связано одинаковое количество информации равное I^(A) =Iog₂ N. Формировать признак конца знака не требуется, поэтому для определения длины кода можно воспользоваться формулой К(А,2) > Iog₂ N. Приемное устройство просто отсчитывает оговоренное заранее количество элементарных сигналов и интерпретирует цепочку (устанавливает, какому знаку она соответствует), соотнося ее с таблицей кодов. Правда, при этом недопустимы сбои, например, пропуск (непрочтение) одного элементарного сигнала приведет к сдвигу всей кодовой последовательности и неправильной ее интерпретации; решается проблема путем синхронизации передачи или иными способами, о которых пойдет речь в гл. 5. С другой стороны, применение равномерного кода оказывается одним из средств контроля правильности передачи, поскольку факт поступления лишнего элементарного сигнала или, наоборот, поступление неполного кода сразу интерпретируется как ошибка.

Примером равномерного алфавитного кодирования является телеграфный код Бодо, пришедший на смену азбуке Морзе. Исходный алфавит должен содержать не более 32-х символов; тогда K(A, 2)=log₂ 32=5,т.е. каждый знак первичного алфавита содержит 5 бит информации и кодируется цепочкой из 5 двоичных знаков. Условие N≤ 32, очевидно, выполняется для языков, основанных на латинском алфавите (N = 27 = 26+ "пробел"), однако в русском алфавите 34 буквы (с пробелом) - именно по этой причине пришлось "сжать" алфавит (как в коде Хаффмана) и объединить в один знак "е" и "ё", а также "ь" и "ъ", что видно из табл. 3.1. После такого сжатия N = 32, однако, не остается свободных кодов для знаков препинания, поэтому в телеграммах они отсутствуют или заменяются буквенными аббревиатурами; это не является заметным ограничением, поскольку, как указывалось выше, избыточность языка позволяет легко восстановить информационное содержание сообщения. Избыточность кода Бодо для русского языка Q(r,2) = 0,148, для английского Q(e,2) = 0,239.

Другим важным для нас примером использования равномерного алфавитного кодирования является представление символьной (знаковой) информации в компьютере. Чтобы определить длину кода, необходимо начать с установления количество знаков в первичном алфавите. Компьютерный алфавит должен включать:

• 26 х 2 = 52 букв латинского алфавита (с учетом прописных и строчных);
• 33 × 2 = 66 букв русского алфавита;
• цифры 0...9 - всего 10;
• знаки математических операций, знаки препинания, спецсимволы ~ 20.

Получаем, что общее число символов N≈ 148. Теперь можно оценить длину кодовой цепочки: К(с,2) ≥ Iog₂148 ≥ 7,21. Поскольку длина кода выражается целым числом, очевидно, К(с,2) = 8. Именно такой способ кодирования принят в компьютерных системах: любому символу ставится в соответствие код из 8 двоичных разрядов (8 бит). Эта последовательность сохраняется и обрабатывается как единое целое (т.е. отсутствует доступ к отдельному биту) - по этой причине разрядность устройств компьютера, предназначенных для хранения или обработки информации, кратна 8. Совокупность восьми связанных бит получила название байт, а представление таким образом символов - байтовым кодированием.

Байт наряду с битом может использоваться как единица измерения количества информации в сообщении. Один байт соответствует количеству информации в одном знаке алфавита при их равновероятном распределении. Этот способ измерения количества информации называется также объемным. Пусть имеется некоторое сообщение (последовательность знаков); оценка количества содержащейся в нем информации согласно рассмотренному ранее вероятностному подходу (с помощью формулы Шеннона (2.17)) дает I_вер, а объемная мера пусть равна 1об; соотношение между этими величинами вытекает из (2.7):

I_вер≤I_об.

Именно байт принят в качестве единицы измерения количества информации в международной системе единиц СИ. 1 байт = 8 бит. Наряду с байтом для измерения количества информации используются более крупные производные единицы:

1 Кбайт = 2¹⁰ байт = 1024 байт (килобайт)

1 Мбайт = 2²⁰ байт = 1024 Кбайт (мегабайт)

1 Гбайт = 2³⁰ байт = 1024 Мбайт (гигабайт)

1 Тбайт = 2⁴⁰ байт = 1024 Гбайт (терабайт)

Использование 8-битных цепочек позволяет закодировать 2⁸=256 символов, что превышает оцененное выше N и, следовательно, дает возможность употребить оставшуюся часть кодовой таблицы для представления дополнительных символов.

Однако недостаточно только условиться об определенной длине кода. Ясно, что способов кодирования, т.е. вариантов сопоставления знакам первичного алфавита восьмибитных цепочек, очень много. По этой причине для совместимости технических устройств и обеспечения возможности обмена информацией между многими потребителями требуется согласование кодов. Подобное согласование осуществляется в форме стандартизации кодовых таблиц.

Первым таким международным стандартом, который применялся на больших вычислительных машинах, был EBCDIC (Extended Binary Coded Decimal Interchange Code) - "расширенная двоичная кодировка десятичного кода обмена". В персональных компьютерах и телекоммуникационных системах применяется международный байтовый код ASCII (American Standard Code for Information Interchange - "американский стандартный код обмена информацией").

Он регламентирует коды первой половины кодовой таблицы (номера кодов от 0 до 127, т.е. первый бит всех кодов 0). В эту часть попадают коды прописных и строчных английских букв, цифры, знаки препинания и математических операций, а также некоторые управляющие коды (номера от 0 до 31), вырабатываемые при использовании клавиатуры. Ниже приведены некоторые /ASC-коды:

Вторая часть кодовой таблицы - она считается расширением основной - охватывает коды в интервале от 128 до 255 (первый бит всех кодов 7). Она используется для представления символов национальных алфавитов (например, русского), а также символов псевдографики. Для этой части также имеются стандарты, например, для символов русского языка это КОИ-8, КОИ-7 и др.

Как в основной таблице, так и в ее расширении коды букв и цифр соответствуют их лексикографическому порядку (т.е. порядку следования в алфавите) - это обеспечивает возможность автоматизации обработки текстов и ускоряет ее.

В настоящее время появился и находит все более широкое применение еще один международный стандарт кодировки - Unicode. Его особенность в том, что в нем использовано 16-битное кодирование, т.е. для представления каждого символа отводится 2 байта. Такая длина кода обеспечивает включения в первичный алфавит 65536 знаков. Это, в свою очередь, позволяет создать и использовать единую для всех распространенных алфавитов кодовую таблицу.

3.2.3. Алфавитное кодирование с неравной длительностью
элементарных сигналов. Код Морзе

В качестве примера использования данного варианта кодирования рассмотрим телеграфный код Морзе ("азбука Морзе"). В нем каждой букве или цифре сопоставляется некоторая последовательность кратковременных импульсов - точек и тире, разделяемых паузами. Длительности импульсов и пауз различны: если продолжительность импульса, соответствующего точке, обозначить т, то длительность импульса тире составляет Зт, длительность паузы между точкой и тире т, пауза между буквами слова Зт (длинная пауза), пауза между словами (пробел) - 6т. Таким образом, под знаками кода Морзе следует понимать: "•" - "короткий импульс + короткая пауза", "- " - "длинный импульс + короткая пауза", "О" - "длинная пауза", т.е. код оказывается троичным.

Свой код Морзе разработал в 1838 г., т.е. задолго до исследований относительной частоты появления различных букв в текстах. Однако им был правильно выбран принцип кодирования - буквы, которые встречаются чаще, должны иметь более короткие коды, чтобы сократить общее время передачи. Относительные частоты букв английского алфавита он оценил простым подсчетом литер в ячейках типографской наборной машины. Поэтому самая распространенная английская буква "Е" получила код "точка". При составлении кодов Морзе для букв русского алфавита учет относительной частоты букв не производился, что, естественно, повысило его избыточность. Как и в рассмотренных ранее вариантах кодирования, произведем оценку избыточности. По-прежнему для удобства сопоставления данные представим в формате табл. 3.1. (см. табл. 3.3.). Признак конца буквы ("О") в их кодах не отображается, но учтен в величине k_i-длине кода буквы i.

Таблица 3.3

Среднее значение длины кода K(r,3) =3,361. Полагая появление знаков вторичного алфавита равновероятным, получаем среднюю информацию на знак равной I⁽²⁾ = Iog₂3 = 1,585 бит.

Подставляя эти данные, а также для русского алфавита I^(r)₁=4,356 бит в β.4), получаем:

Q(кб2) =(3,361 -1,585)74,356 - 1 - 0,223,

т.е. избыточность составляет около 22% (для английского языка ~ 19%). Тем не менее, код Морзе имел в недалеком прошлом весьма широкое распространение в ситуациях, когда источником и приемником сигналов являлся человек (не техническое устройство) и на первый план выдвигалась не экономичность кода, а удобство его восприятия человеком.

Поиск по сайту: