Оптимальное кодирование

Оптимальное кодирование обладает определенными свойствами, которые можно использовать для его построения.

ЛЕММА Пусть - схема оптимального кодирования для распределения вероятностей . Тогда если p_i>p_j, то .

Доказательство

От противного. Пусть i<j, p_i>p_j и l_i>l_j. Тогда рассмотрим

Имеем:

что противоречит тому, что оптимально.

Таким образом, не ограничивая общности, можно считать, что .

ЛЕММА

Если - схема оптимального префиксного кодирования для распределения вероятностей , то среди элементарных кодов, имеющих максимальную длину, имеются два, которые различаются только во последнем разряде.

Доказательство

От противного

1. Пусть кодовое слово максимальной длины одно и имеет вид , где b=0 V b=1. Имеем: . Так как схема префиксная, то слова 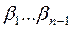не являются префиксами 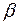. С другой стороны, 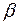не является префиксом слов 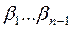, иначе было бы 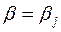, а значит, было бы префиксом . Тогда схема тоже префиксная, причем , что противоречит оптимальности .

2. Пусть теперь два кодовых слова и 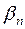максимальной длины отличаются не в последнем разряде, то есть , причем не являются префиксами для и наоборот. Тогда схема также является префиксной, причем , что противоречит оптимальности .

ТЕОРЕМА Если - схема оптимального префиксного кодирования для распределения вероятностей и , причем

,

то кодирование со схемой

является оптимальным префиксным кодированием для распределения вероятностей P_n=p₁,…,p_j-1,p_j+1,…,p_n-1,q’,q’’.

Доказательство

1. Если было префиксным, то тоже будет префиксным по построению.
2. 

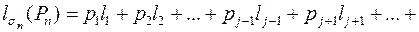
1. Пусть схема оптимальна для P_n. Тогда по предшествуюещй лемме . Положим и рассмотрим схему , где j определено так, чтобы .
2. 

5. - префиксное, значит тоже префиксное.

6. - оптимально, значит, .

7. , но - оптимально, значит оптимально.

Поиск по сайту: