Глава 6. Кодирование

Вопросы кодирования издавна играли заметную роль в математике.

Пример

1. Десятичная позиционная система счисления – это способ кодирования натуральных чисел. Римские цифры – другой способ кодирования натуральных чисел, причем гораздо более наглядный и естественный: палец – I, пятерня – V, две пятерки – X. Однако при этом способе кодирования труднее выполнять арифметические операции надо большими числами, поэтому он был вытеснен позиционной десятичной системой.
2. Декартовы координаты – способ кодирования геометрических объектов числами.

Ранее средства кодирования играли вспомогательную роль и не рассматривались как отдельный предмет математического изучения, но с появлением компьютеров ситуация радикально изменилась. Кодирование буквально пронизывает информационные технологии и является центральным вопросом при решении самых разных (практически всех) задач программирования:

1. представление данных произвольной природы (например, чисел, текста, графики) в памяти компьютера;
2. защита информации от несанкционированного доступа;
3. обеспечение помехоустойчивости при передаче данных по каналам связи;
4. сжатие информации в базах данных

ЗАМЕЧАНИЕ

Само составление текста программы часто и совершенно справедливо называют кодированием.

Не ограничивая общности, задачу кодирования можно сформулировать следующим образом. Пусть заданы алфавиты , и функция , где S – некоторое множество слов в алфавите А, S 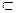A^*. Тогда функция F называется кодированием, элементы множества S – сообщениями, а элементы 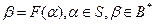- кодами (соответствующих сообщений). Обратная функция F^-1 (если она существует!) называется декодированием.

Если |B|=m, то F называется m-ичным кодированием. Наиболее распространенный случай B={0, 1} – двоичное кодирование. Именно этот случай рассматривается в последующих разделах; слово «двоичное» опускается.

Типичная задача теории кодирования формулируется следующим образом: при заданных алфавитах А, В и множестве сообщений S найти такой кодирование F, которое обладает определенными свойствами (то есть удовлетворяет заданным ограничениям) и оптимально в некотором смысле. Критерии оптимальности, как правило, связан с минимизацией длин кодов. Свойства, которые требуются от кодирования, бывают само разнообразной природы:

· существование декодирования – это очень естественное свойство, однако даже оно требуется не всегда. Например, трансляция программы на языке высокого уровня в машинные команды – это кодирование, для которого не требуется однозначного декодирования;

· помехоустойчивость, или исправление ошибок: функция декодирования F^-1 обладает таким свойством, что , если в определенном смысле близко к .

· заданная сложность (или простота) кодирования и декодирования. Например, в криптографии изучаются такие способы кодирования, при которых имеется просто вычисляемая функция F, но определение функции F^-1 требует очень сложных вычислений.

Большое значения для задач кодирования имеет природа множества сообщений S. При одних и тех же алфавитах А, В и требуемых свойствах кодирования F оптимальные решения могут кардинально отличаться для разных S. Для описания множества S (как правило, очень большого или бесконечного) применяются различные методы:

· теоретико –множественное описание, например ;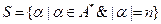

· вероятностное описание, например S=A^*, и заданы вероятности p_i появления букв в сообщении, ;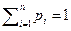

· логико-комбинаторное описание, например, S задано порождающей формальной грамматикой.

Поиск по сайту: