 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
B7 (повышенный уровень, время – 2 мин)
Тема: Кодирование чисел. Системы счисления.
Что нужно знать:
· принципы кодирования чисел в позиционных системах счисления
·  чтобы перевести число, скажем, 12345N, из системы счисления с основанием
чтобы перевести число, скажем, 12345N, из системы счисления с основанием  в десятичную систему, нужно умножить значение каждой цифры на
в десятичную систему, нужно умножить значение каждой цифры на  в степени, равной ее разряду:
в степени, равной ее разряду:
4 3 2 1 0 ← разряды
1 2 3 4 5N = 1·N4 + 2·N3 + 3·N2 + 4·N1 + 5·N0
· последняя цифра записи числа в системе счисления с основанием  – это остаток от деления этого числа на
– это остаток от деления этого числа на 
· две последние цифры – это остаток от деления на  , и т.д.
, и т.д.
Пример задания:
Решите уравнение  .
.
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
Решение:
1) удобнее всего перевести все числа в десятичную систему, решить уравнение и результат перевести в шестеричную систему
2) получаем 
3) уравнение приобретает вид  , откуда получаем
, откуда получаем 
4) переводим 15 в шестеричную систему счисления: 
5) ответ: 23.
Ещё пример задания:
Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Решение:
6) если запись числа в системе счисления с основанием N заканчивается на 0, то это число делится на N нацело
7) поэтому в данной задаче требуется найти наименьшее натуральное число, которое делится одновременно на 3 и на 5, то есть, делится на 15
8) очевидно, что это число 15.
Ещё пример задания:
Запись числа 6710 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание этой системы счисления N.
Решение:
9) поскольку запись в системе счисления с основанием N заканчивается на 1, то остаток от деления числа 67 на N равен 1, то есть при некотором целом  имеем
имеем

10) следовательно, основание N – это делитель числа 66
11) с другой стороны, запись числа содержит 4 цифры, то есть 
12) выпишем кубы и четвертые степени первых натуральных чисел, которые являются делителями числа 66:

13) видим, что из этого списка только для числа N = 3 выполняется условие 
14) таким образом, верный ответ – 3.
15) можно сделать проверку, переведя число 67 в троичную систему 6710 = 21113
Еще пример задания:
Запись числа 38110 в системе счисления с основанием N оканчивается на 3 и содержит 3 цифры. Укажите наибольшее возможное основание этой системы счисления N.
Решение:
1) поскольку запись в системе счисления с основанием N заканчивается на 3, то остаток от деления числа 381 на N равен 3, то есть при некотором целом  имеем
имеем

2) следовательно, основание N – это делитель числа 
3) с другой стороны, запись числа содержит 3 цифры, то есть 
4) неравенство  дает
дает  (так как
(так как  )
)
5) неравенство  дает
дает  (так как
(так как  )
)
6) таким образом,  ; в этом диапазоне делителями числа 378 являются числа
; в этом диапазоне делителями числа 378 являются числа
· 9, при  получаем запись числа
получаем запись числа 
· 14, при  получаем запись числа
получаем запись числа 
· 18, при  получаем запись числа
получаем запись числа 
7) наибольшим из приведенных чисел – это 18 (можно было сразу искать подбором наибольший делитель числа 378, начиная с 19 «вниз», на уменьшение)
8) таким образом, верный ответ – 18.
Еще пример задания:
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Общий подход:
· вспомним алгоритм перевода числа из десятичной системы в систему с основанием  (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на
(см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на  , а две младших цифры – это остаток от деления на
, а две младших цифры – это остаток от деления на  и т.д.
и т.д.
· в данном случае  , остаток от деления числа на
, остаток от деления числа на  должен быть равен 114 = 5
должен быть равен 114 = 5
· потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16
Решение (вариант 1, через десятичную систему):
1) общий вид чисел, которые дают остаток 5 при делении на 16:

где  – целое неотрицательное число (0, 1, 2, …)
– целое неотрицательное число (0, 1, 2, …)
2) среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при  ) и 21 (при
) и 21 (при  )
)
3) таким образом, верный ответ – 5, 21.
Возможные ловушки и проблемы:
· выражение «не превосходящие  » означает «меньшие или равные » означает «меньшие или равные  », а не строго меньшие », а не строго меньшие  · остаток, состоящий из нескольких цифр (здесь – 114), нужно не забыть перевести в десятичную систему
· найденные числа нужно записать именно в порядке возрастания, как требуется
· остаток, состоящий из нескольких цифр (здесь – 114), нужно не забыть перевести в десятичную систему
· найденные числа нужно записать именно в порядке возрастания, как требуется
|
Решение (вариант 2, через четверичную систему, предложен О.А. Тузовой):
1) переведем 25 в четверичную систему счисления: 25 = 1214, все интересующие нас числа не больше этого значения
2) из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два:
это 114 = 5 и 1114 = 21
3) таким образом, верный ответ – 5, 21.
| Возможные ловушки и проблемы: · есть риск случайно «забыть» какое-то число или найти «лишнее» (в данном случае – большее 25) · можно сделать ошибки при переводе чисел из четверичной системы в десятичную или вообще «забыть» перевести |
Еще пример задания:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Общий подход:
· здесь обратная задача – неизвестно основание системы счисления, мы обозначим его через 
· поскольку последняя цифра числа – 2, основание должно быть больше 2, то есть 
· вспомним алгоритм перевода числа из десятичной системы в систему с основанием  (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на
(см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на 
Решение:
1) итак, нужно найти все целые числа  , такие что остаток от деления 23 на
, такие что остаток от деления 23 на  равен 2, или (что то же самое)
равен 2, или (что то же самое)
 (*)
(*)
где  – целое неотрицательное число (0, 1, 2, …);
– целое неотрицательное число (0, 1, 2, …);
2) сложность в том, что и  , и
, и  неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
3) из формулы (*) получаем  , так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2
, так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2
4) в этой задаче есть только три таких делителя:  и
и 
5) таким образом, верный ответ – 3, 7, 21.
Возможные ловушки и проблемы:
· нужно учесть, что основание системы счисления должно быть больше любой цифры числа, поэтому делитель  не подходит (должно быть не подходит (должно быть  )
· числа нужно записывать в ответе в порядке возрастания, как требуется по условию )
· числа нужно записывать в ответе в порядке возрастания, как требуется по условию
|
Еще пример задания:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 11.
Общий подход:
· неизвестно основание системы счисления, мы обозначим его через 
· пока будем считать, что запись числа 31 в системе с основанием  состоит из трех цифр, причем две младшие (11) нам даны, а одну (обозначим ее через
состоит из трех цифр, причем две младшие (11) нам даны, а одну (обозначим ее через  ) нужно найти:
) нужно найти:
2 1 0 ← разряды
31 = k 1 1N = k·N2 + N1 + N0 = k·N2 + N + 1
· можно показать, что при большем количестве разрядов эта формула также верна, то есть, число 31 можно представить как  при некотором целом
при некотором целом  ; например, для числа с пятью разрядами получаем:
; например, для числа с пятью разрядами получаем:
4 3 2 1 0 ← разряды
31 = k4 k3 k2 1 1N = k4·N4 + k3·N3 + k2·N2 + N1 + N0
= k·N2 + N + 1
для  (из первых трех слагаемых вынесли общий множитель
(из первых трех слагаемых вынесли общий множитель  )
)
Решение:
1) итак, нужно найти все целые числа  , такие что
, такие что
 (**)
(**)
где  – целое неотрицательное число (0, 1, 2, …);
– целое неотрицательное число (0, 1, 2, …);
2) сложность в том, что и  , и
, и  неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
3) из формулы (**) получаем  , так что задача сводится к тому, чтобы найти все делители
, так что задача сводится к тому, чтобы найти все делители  числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом
числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом  , то есть,
, то есть,  – целое число
– целое число
4) выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30
5) из всех этих делителей только для 2, 3, 5 и 30 значение  – целое число (оно равно соответственно 7, 3, 1 и 0)
– целое число (оно равно соответственно 7, 3, 1 и 0)
6) таким образом, верный ответ – 2, 3, 5, 30.
Еще пример задания:
Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12, …, 17 в системе счисления с основанием 5.
Решение (вариант 1):
1) запишем первое и последнее число в заданном диапазоне в системе счисления с основанием 5:
10 = 205, 17 = 325 .
2) заметим, что оба они содержат цифру 2, так что, 2 цифры мы уже нашли
3) между 205 и 325 есть еще числа
215, 225, 235, 245, 305, 315.
4) в них 5 цифр 2 (в числе 225 – сразу две двойки), поэтому всего цифра 2 встречается 7 раз
5) таким образом, верный ответ – 7.
| Возможные ловушки и проблемы: · нужно не забыть, что в системе счисления с основанием 5 старшая цифра – 4, то есть, вслед за 245 следует 305 · помните, что нужно определить не количество чисел, в которых есть двойка, а количество самих двоек · можно не обратить внимание на то, что в числе 225 цифра 2 встречается 2 раза |
Решение (вариант 2):
1) переведем все указанные числа в систему счисления с основанием 5:
10 = 205, 11 = 215, 12 = 225, 13 = 235, 14 = 245, 15 = 305, 16 = 315, 17 = 325 .
2) считаем цифры 2 – получается 7 штук
3) таким образом, верный ответ – 7.
Еще пример задания:
Укажите наименьшее основание системы счисления, в которой запись числа 30 трехзначна.
Решение:
1) обозначим через  неизвестное основание системы счисления, тогда запись числа 30 в этой системе имеет вид
неизвестное основание системы счисления, тогда запись числа 30 в этой системе имеет вид

2) вспомним алгоритм перевода числа из системы счисления с основанием  в десятичную систему: расставляем сверху номера разрядов и умножаем каждую цифру на основание в степени, равной разряду:
в десятичную систему: расставляем сверху номера разрядов и умножаем каждую цифру на основание в степени, равной разряду:

3) поскольку запись трехзначная,  , поэтому
, поэтому 
4) с другой стороны, четвертой цифры нет, то есть, в третьем разряде – ноль, поэтому 
5) объединяя последние два условия, получаем, что искомое основание  удовлетворяет двойному неравенству
удовлетворяет двойному неравенству

6) учитывая, что  – целое число, методом подбора находим целые решения этого неравенства; их два – 4 и 5:
– целое число, методом подбора находим целые решения этого неравенства; их два – 4 и 5:


7) минимальное из этих значений – 4
8) таким образом, верный ответ – 4.
Решение (без подбора):
1) выполним п.1-4 так же, как и в предыдущем варианте решения
2) найдем первое целое число, куб которого больше 30; это 4, так как

3) проверяем второе неравенство:  , поэтому в системе счисления с основанием 4 запись числа 30 трехзначна
, поэтому в системе счисления с основанием 4 запись числа 30 трехзначна
4) таким образом, верный ответ – 4.
Еще пример задания:
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 начинается на 3?
Решение (вариант 1):
1) нас интересуют числа от 1 до 30
2) сначала определим, сколько цифр может быть в этих числах, записанных в системе счисления с основанием 5
3) поскольку  , в интересующих нас числах может быть от 1 до 3 цифр
, в интересующих нас числах может быть от 1 до 3 цифр
4) рассмотрим трехзначные числа, начинающиеся на 3 в системе с основанием 5:

все они заведомо не меньше  , поэтому в наш диапазон не попадают;
, поэтому в наш диапазон не попадают;
5) таким образом, остается рассмотреть только однозначные и двухзначные числа
6) есть всего одно однозначное число, начинающееся на 3, это 3
7) общий вид всех двузначных чисел, начинающихся на 3 в системе с основанием 5:

где  – целое число из множества {0, 1, 2,3,4} (поскольку система счисления имеет основание 5 и цифр, больших 4, в записи числа быть не может)
– целое число из множества {0, 1, 2,3,4} (поскольку система счисления имеет основание 5 и цифр, больших 4, в записи числа быть не может)
8) используя эту формулу, находим интересующие нас двузначные числа – 15, 16, 17, 18 и 19
9) таким образом, верный ответ – 3, 15, 16, 17, 18, 19.
Решение (вариант 2, предложен Сенькиной Т.С., г. Комсомольск-на-Амуре):
1) нас интересуют числа от 1 до 30; сначала определим, сколько цифр может быть в пятеричной записи эти чисел
2) поскольку  , в интересующих нас числах может быть не более 2 цифр (все трехзначные пятеричные числа, начинающиеся с 3, больше 30)
, в интересующих нас числах может быть не более 2 цифр (все трехзначные пятеричные числа, начинающиеся с 3, больше 30)
3) есть всего одно однозначное число, начинающееся на 3, это 3
4) выпишем все пятеричные двузначные числа, которые начинаются с 3, и переведем их в десятичную систему: 305 = 15, 315 = 16, 325 = 17, 335 = 18 и 345 = 19
5) таким образом, верный ответ – 3, 15, 16, 17, 18, 19.
Еще пример задания:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.
Решение (1 способ):
1) Если число в системе с основанием  оканчивается на 13, то
оканчивается на 13, то
а)  , потому что в системах с меньшим основанием нет цифры 3
, потому что в системах с меньшим основанием нет цифры 3
б) это число можно представить в виде  , где
, где  – целое неотрицательное число
– целое неотрицательное число
2) определим наибольшее возможное  с учетом условия
с учетом условия  . Из уравнения
. Из уравнения  следует
следует  .
.
3) очевидно, что чем меньше  , тем больше
, тем больше  , поэтому значение
, поэтому значение  не превышает
не превышает 
здесь мы подставили  – наименьшее допустимое значение
– наименьшее допустимое значение 
4) остается перебрать все допустимые значения  (от 0 до
(от 0 до  ), решая для каждого из них уравнение
), решая для каждого из них уравнение
 или равносильное
или равносильное 
относительно  , причем нас интересуют только натуральные числа
, причем нас интересуют только натуральные числа 
5) получаем
а) при  :
: 
б) при  : решения – не целые числа
: решения – не целые числа
в) при  :
:  и
и  , второе решение не подходит
, второе решение не подходит
6) таким образом, верный ответ: 4, 68.
Решение (2 способ, М.В. Кузнецова и её ученики):
1) запись числа71 в системе с основанием  оканчивается на 13, т.е. в разряде единиц – 3, это значит, что остаток от деления 71 на
оканчивается на 13, т.е. в разряде единиц – 3, это значит, что остаток от деления 71 на  равен 3, то есть для некоторого целого
равен 3, то есть для некоторого целого  имеем
имеем

2) таким образом, искомые основания – делители числа 68; остается выбрать из них те, которые соответствуют другим условиям задачи
3) среди чисел, оканчивающихся на 13 в системе счисления с основанием  ,минимальное – это само число
,минимальное – это само число  ; отсюда найдем максимальное основание:
; отсюда найдем максимальное основание:

так что первый ответ: 68.
4) остальные числа, окачивающиеся в этой системе на 13, имеют не менее 3-х знаков ( ,
,  …), т.е. все они больше
…), т.е. все они больше 
5) поэтому  , следовательно,
, следовательно, 
6) по условию в записи числа есть цифра 3, поэтому  (в системах с основанием £ 3 цифры 3 нет)
(в системах с основанием £ 3 цифры 3 нет)
7) итак:  , и при этом
, и при этом  – делитель 68; единственное возможное значение
– делитель 68; единственное возможное значение  (на 5,6,7 и 8 число 68 не делится)
(на 5,6,7 и 8 число 68 не делится)
8) таким образом, верный ответ: 4, 68.
| Возможные ловушки и проблемы: · на шаге 1 нужно вычесть из числа только число единиц, то есть младшую из двух заданных цифр (в примере – 3) · можно забыть рассмотреть двузначное число, записанное заданными в условии цифрами (в примере – 13x), и пропустить максимальное основание · нужно помнить, что а) максимальная цифра на 1 меньше основания системы счисления б) 100 в системе с основанием p равно p2 |
Еще пример задания:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 86 оканчивается на 22.
Решение (1 способ):
1) Если число в системе с основанием  оканчивается на 22, то
оканчивается на 22, то
а)  , потому что в системах с меньшим основанием нет цифры 3
, потому что в системах с меньшим основанием нет цифры 3
б) это число можно представить в виде  , где
, где  – целое неотрицательное число
– целое неотрицательное число
2) определим наибольшее возможное  с учетом условия
с учетом условия  . Из уравнения
. Из уравнения  следует
следует  .
.
3) очевидно, что чем меньше  , тем больше
, тем больше  , поэтому значение
, поэтому значение  не превышает
не превышает 
здесь мы подставили  – наименьшее допустимое значение
– наименьшее допустимое значение 
4) остается перебрать все допустимые значения  (от 0 до
(от 0 до  ), решая для каждого из них уравнение
), решая для каждого из них уравнение
 или равносильное
или равносильное 
относительно  , причем нас интересуют только натуральные числа
, причем нас интересуют только натуральные числа 
5) получаем
а) при  :
: 
б) при  : решения – не целые числа
: решения – не целые числа
в) при  :
:  и
и  , второе решение не подходит
, второе решение не подходит
г) при  : решения – не целые числа
: решения – не целые числа
6) таким образом, верный ответ: 6, 42.
Решение (2 способ, М.В. Кузнецова и её ученики):
1) запись числа 86 в системе с основанием  оканчивается на 22, т.е. в разряде единиц – 2, это значит, что остаток от деления 86 на
оканчивается на 22, т.е. в разряде единиц – 2, это значит, что остаток от деления 86 на  равен 2, то есть для некоторого целого
равен 2, то есть для некоторого целого  имеем
имеем

2) таким образом, искомые основания – делители числа 84; остается выбрать из них те, которые соответствуют другим условиям задачи
3) среди чисел, оканчивающихся на 22 в системе счисления с основанием  ,минимальное – это само число
,минимальное – это само число  ; отсюда найдем максимальное основание:
; отсюда найдем максимальное основание:

так что первый ответ: 42.
4) остальные числа, окачивающиеся в этой системе на 22, имеют не менее 3-х знаков ( ,
,  …), т.е. все они больше
…), т.е. все они больше 
5) поэтому  , следовательно,
, следовательно, 
6) по условию в записи числа есть цифра 2, поэтому 
7) итак:  , и при этом
, и при этом  – делитель 84; возможные значения
– делитель 84; возможные значения  (на 5,8 и 9 число 84 не делится)
(на 5,8 и 9 число 84 не делится)
8) переводя число 86 в системы счисления с основаниями  , находим, что только для основания 6 запись числа оканчивается на 22 (при делении на 3, 4 и 7 «вторые» остатки не равны 2):
, находим, что только для основания 6 запись числа оканчивается на 22 (при делении на 3, 4 и 7 «вторые» остатки не равны 2):
| Дальше делить нет смысла | |||||||||||||||||||||||||||||||||
| 9… | 5… | ||||||||||||||||||||||||||||||||
| 1 | 1 | 5 |
9) таким образом, верный ответ: 6, 42.
Еще пример задания:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 94 начинается на 23.
Решение:
1) Из условия сразу видно, что искомое основание не меньше 4 (в записи есть цифра 3).
2) Если запись числа 94 в некоторой системе счисления с основанием  двузначна (94 = 23x), то справедливо равенство
двузначна (94 = 23x), то справедливо равенство  ; нас интересуют натуральные решения этого уравнения, такие что
; нас интересуют натуральные решения этого уравнения, такие что  , таких решений нет.
, таких решений нет.
3) Предположим, что число четырехзначное. Минимальное допустимое четырехзначное число – 2300x, где  . При минимальном основании (
. При минимальном основании ( ) оно равно
) оно равно  , поэтому запись нужного нам числа имеет не больше трех знаков.
, поэтому запись нужного нам числа имеет не больше трех знаков.
4) На основании (2) и (3) делаем вывод, что число трехзначное, то есть  , где
, где  – целое неотрицательное число, такое что
– целое неотрицательное число, такое что  .
.
5) Максимальное  можно определить как решение уравнения
можно определить как решение уравнения  (при
(при  ); получаем одно из решений – 6,15; поэтому
); получаем одно из решений – 6,15; поэтому 
6) Если мы знаем  , то
, то  определится как
определится как  ; пробуем подставлять в эту формулу
; пробуем подставлять в эту формулу  , пытаясь получить
, пытаясь получить 
7) Минимальное  будет при
будет при  :
:  , а при
, а при  получается
получается 
8) Таким образом, верный ответ: 6.
Еще пример задания:
Найти сумму восьмеричных чисел 178 +1708 +17008 +...+17000008, перевести в 16-ую систему счисления. Найдите в записи числа, равного этой сумме, третью цифру слева.
Решение:
1) Несложно выполнить прямое сложение восьмеричных чисел, там быстро обнаруживается закономерность:
178 + 1708 = 2078
178 + 1708 + 17008 = 21078
178 + 1708 + 17008 + 170008 = 211078
178 + 1708 + 17008 + 170008 + 1700008 = 2111078
178 + 1708 + 17008 + 170008 + 1700008 + 17000008 = 21111078
2) Переведем последнюю сумму через триады в двоичный код (заменяем каждую восьмеричную цифру на 3 двоичных):
100010010010010001112
3) Теперь разбиваем цепочку на тетрады (группы из 4-х двоичных цифр), начиная справа, и каждую тетраду представляем в виде шестнадцатеричной цифры
100010010010010001112
8 9 2 4 7
4) Таким образом, верный ответ (третья цифра слева): 2.
Еще пример задания:
Чему равно наименьшее основание позиционной системы счисления  , при котором 225x = 405y? Ответ записать в виде целого числа.
, при котором 225x = 405y? Ответ записать в виде целого числа.
Решение:
1) Поскольку в левой и в правой частях есть цифра 5, оба основания больше 5, то есть перебор имеет смысл начинать с  .
.
2) Очевидно, что  , однако это не очень нам поможет.
, однако это не очень нам поможет.
3) Для каждого «подозреваемого»  вычисляем значение
вычисляем значение  и решаем уравнение
и решаем уравнение  , причем нас интересуют только натуральные
, причем нас интересуют только натуральные  .
.
4) Для  и
и  нужных решений нет, а для
нужных решений нет, а для  получаем
получаем
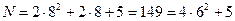
так что 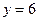 .
.
5) Таким образом, верный ответ (минимальное значение  ): 8.
): 8.
Еще пример задания:
Запись числа 3010 в системе счисления с основанием N оканчивается на 0 и содержит 4 цифры. Чему равно основание этой системы счисления N?
Решение (1 способ, подбор):
1) запись числа 30 в системе с основанием N длиннее, чем в десятичной (4 цифры против двух), поэтому основание N меньше 10
2) это дает шанс решить задачу методом подбора, переводя в разные системы, начиная с N = 2 до N = 9
3) переводим:
30 = 111102 = 10103 = …
4) дальше можно не переводить, поскольку запись 10103 удовлетворяет условию: заканчивается на 0 и содержит 4 цифры
5) можно проверить, что при N ≥ 4 запись числа 30 содержит меньше 4 цифр, то есть не удовлетворяет условию
6) Ответ: 3.
Решение (2 способ, неравенства):
1) запись числа 30 в системе с основанием N содержит ровно 4 цифры тогда и только тогда, когда старший разряд – третий, то есть

2) первая часть двойного неравенства  дает (в целых числах)
дает (в целых числах) 
3) вторая часть неравенства  дает (в целых числах)
дает (в целых числах) 
4) объединяя результаты пп. 2 и 3 получаем, что N = 3
5) заметим, что условие «оканчивается на 0» – лишнее, ответ однозначно определяется по количеству цифр
6) Ответ: 3.
Задачи для тренировки [1]:
1) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
2) В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.
3) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 39 оканчивается на 3.
4) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
5) В системе счисления с некоторым основанием десятичное число 129 записывается как 1004. Укажите это основание.
6) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 40 оканчивается на 4.
7) В системе счисления с некоторым основанием число десятичное 25 записывается как 100. Найдите это основание.
8) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 27 оканчивается на 3.
9) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 26, запись которых в троичной системе счисления оканчивается на 22?
10) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в четверичной системе счисления оканчивается на 31?
11) Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры?
12) Укажите, сколько всего раз встречается цифра 3 в записи чисел 19, 20, 21, …, 33 в системе счисления с основанием 6.
13) Укажите, сколько всего раз встречается цифра 1 в записи чисел 12, 13, 14, …, 31 в системе счисления с основанием 5.
14) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 1.
15) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 63 оканчивается на 23.
16) Десятичное число, переведенное в восьмеричную и в девятеричную систему, в обоих случаях заканчивается на цифру 0. Какое минимальное натуральное число удовлетворяет этому условию?
17) В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
18) Укажите наименьшее основание системы счисления, в которой запись числа 70 трехзначна.
19) Укажите наименьшее основание системы счисления, в которой запись числа 50 двузначна.
20) Сколько значащих цифр в записи десятичного числа 357 в системе счисления с основанием 7?
21) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием 6 начинается на 4?
22) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 20, запись которых в системе счисления с основанием 3 начинается на 2?
23) Какое десятичное число при записи в системе счисления с основанием 5 представляется как 12345?
24) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101?
25) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 30 оканчивается на 8.
26) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4.
27) В системе счисления с некоторым основанием десятичное число 83 записывается в виде 123. Укажите это основание.
28) В системе счисления с некоторым основанием десятичное число 144 записывается в виде 264. Укажите это основание.
29) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 32 оканчивается на 4.
30) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 27, запись которых в двоичной системе счисления оканчивается на 110?
31) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в троичной системе счисления оканчивается на 21?
32) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 45, запись которых в двоичной системе счисления оканчивается на 1010?
33) Десятичное число кратно 16. Какое минимальное количество нулей будет в конце этого числа после перевода его в двоичную систему счисления?
34) В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.
35) Укажите, сколько всего раз встречается цифра 3 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 4.
36) Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.
37) В саду 100 фруктовых деревьев – 14 яблонь и 42 груши. Найдите основание системы счисления, в которой указаны эти числа.
38) Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201.
39) Найдите основание системы счисления, в которой выполнено умножение: 3·213 = 1043.
40) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 20, запись которых в системе счисления с основанием 5 оканчивается на 3?
41) Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 100, запись которых в системе счисления с основанием 5 оканчивается на 11?
42) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.
43) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 84 оканчивается на 14.
44) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 61 оканчивается на 15.
45) Найдите десятичное число x, такое что 20 < x < 30, запись которого в системе счисления с основанием 3 заканчивается на 11.
46) Запись числа 658 в некоторой системе счисления выглядит так: 311q. Найдите основание системы счисления q.
47) Запись числа 30 в некоторой системе счисления выглядит так: 110q. Найдите основание системы счисления q.
48) Запись числа 2B16 в некоторой системе счисления выглядит так: 111q. Найдите основание системы счисления q.
49) Запись числа 23 в некоторой системе счисления выглядит так: 212q. Найдите основание системы счисления q.
50) Запись числа 2105 в некоторой системе счисления выглядит так: 313q. Найдите основание системы счисления q.
51) Укажите наименьшее основание системы счисления, в которой запись числа 50 трехзначна.
52) Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 348 оканчивается на 20.
53) Запись числа 344 в некоторой системе счисления выглядит так: 1A8q. Найдите основание системы счисления q.
54) К записи натурального числа в восьмеричной системе счисления справа приписали два нуля. Во сколько раз увеличилось число? Ответ запишите в десятичной системе счисления.
55) Запись числа 281 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно максимально возможное основание системы счисления?
56) Запись числа 381 в системе счисления с основанием N содержит 3 цифры и оканчивается на 3. Чему равно максимально возможное основание системы счисления?
57) Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
58) Запись числа 256 в системе счисления с основанием N содержит 3 цифры и оканчивается на 4. Чему равно минимально возможное основание системы счисления?
59) Запись числа 325 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно минимально возможное основание системы счисления?
60) Запись числа 180 в системе счисления с основанием N содержит 3 цифры и оканчивается на 0. Перечислите в порядке возрастания все возможные основания системы счисления.
61) Запись числа 280 в системе счисления с основанием N содержит 3 цифры и оканчивается на 0. Перечислите в порядке возрастания все возможные основания системы счисления.
62) Запись натурального числа в системах счисления с основанием 4 и 6 заканчивается на 0. Найдите минимальное натуральное число, удовлетворяющее этим условиям.
63) Десятичное число 71 в некоторой системе счисления записывается как «78». Определите основание системы счисления.
64) Десятичное число 70 в некоторой системе счисления записывается как «64». Определите основание системы счисления.
65) Десятичное число 57 в некоторой системе счисления записывается как «212». Определите основание системы счисления.
66) Десятичное число 109 в некоторой системе счисления записывается как «214». Определите основание системы счисления.
67) Решите уравнение  .
.
Ответ запишите в четверичной системе счисления. Основание системы счисления указывать не нужно.
68) Решите уравнение  .
.
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
69) Решите уравнение  .
.
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
70) Решите уравнение  .
.
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
[1] Источники заданий:
1. Демонстрационные варианты ЕГЭ 2004-2013 гг.
2. Тренировочные работы МИОО.
3. Гусева И.Ю. ЕГЭ. Информатика: раздаточный материал тренировочных тестов. — СПб: Тригон, 2009.
4. Самылкина Н.Н., Островская Е.М. Информатика: тренировочные задания. – М.: Эксмо, 2009.
5. Якушкин П.А., Лещинер В.Р., Кириенко Д.П. ЕГЭ 2010. Информатика. Типовые тестовые задания. — М: Экзамен, 2010.
6. Крылов С.С., Лещинер В.Р., Якушкин П.А. ЕГЭ-2010. Информатика. Универсальные материалы для подготовки учащихся / под ред. В.Р. Лещинера / ФИПИ. — М.: Интеллект-центр, 2010.
7. Якушкин П.А., Ушаков Д.М. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010. Информатика. — М.: Астрель, 2009.
8. М.Э. Абрамян, С.С. Михалкович, Я.М. Русанова, М.И. Чердынцева. Информатика. ЕГЭ шаг за шагом. – М.: НИИ школьных технологий, 2010.
9. Чуркина Т.Е. ЕГЭ 2011. Информатика. Тематические тренировочные задания. — М.: Эксмо, 2010.
10. Информатика и ИКТ: ЕГЭ-2012. – СПб.: Просвещение, 2012.
Поиск по сайту: