Обнаружение ошибки в коде Хэмминга

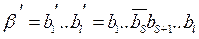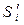Пусть по каналу связи передавался код , на выходе канала связи было принято слово , т.о. произошло искажение s-го разряда. Заметим, что s может быть номером как информационного, так и контрольного разряда. Пусть – запись числа S в двоичной системе исчисления . Сформируем число , двоичные разряды которого вычисляются следующим образом:

есть сумма по модулю 2 содержимого всех разрядов кода на выходе канала связи с номерами, принадлежащими первой последовательности, включая ее первый элемент. При подсчете аналогичное суммирование ведется по 2,…, k -й последовательности.

Теорема. Число является номером искаженного разряда, т.е. .

Доказательство. Покажем, что числа равны, потому что поразрядно равны их двоичные представления, т.е. 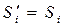для всех .

Пусть . Т.к. в первую последовательность включаются числа, имеющие в двоичном представлении первый разряд, равный 1, то это означает, что S не принадлежит первой последовательности. Это означает также, что все разряды кода с номерами, принадлежащими первой последовательности, не искажены, поэтому получим

, т.к. для разрядов Хэмминга выполняется ( 2.8 ). Таким образом, из того, что следует . Пусть теперь , тогда номер S искаженного разряда принадлежит первой последовательности. Т.к. искаженный разряд кода есть и , получим:

Получим, что из того, что 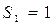следует . Тогда .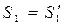

Аналогично доказывается, что .

Замечание. Если при передаче кода нет искажений, то 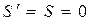. После определения номера S в том случае, когда , производится коррекция ошибки, т.е. 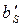заменяется на .

Пример 3. Пусть на вход канала связи поступил код и в нем в результате помех был искажен 6-ой разряд, т.е. на выходе канала связи был получен код 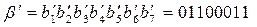. Убедимся, что по коду можно вычислить номер искаженного разряда. Поскольку , то согласно неравенству (2.6) находим , тогда . Вычислим

Следовательно, в двоичной системе счисления, т.е. 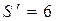. Т.к. , то 6 – номер искаженного разряда. После этого, заменяя в 6-ом разряде 0 на 1, получим код .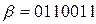

Пример 4. Пусть на выходе канала связи получен код . Определим, было ли искажение при передаче, и если да, то в каком разряде. Т.к. , то из (2.6) получаем . Тогда

Таким образом, , т.е. код был передан без искажений.

Декодирование.

Декодирование состоит в построении исходного сообщения 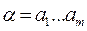по коду . Для этого из кода извлекается содержимое информационных разрядов.

Пример 5. Для кода 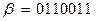информационными являются разряды 3, 5, 6, 7, остальные – контрольные. Отсюда .

Пример 6. Для кода 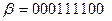информационные разряды – 3, 5, 6, 7, 9. Отсюда .

Поиск по сайту: