Исправление ошибок при передаче избыточным кодом

Обнаружение и исправление ошибок с помощью корректирующих кодов происходит вследствие того, что для передачи информации используются не все M_max = (q)ⁿ возможные кодовые комбинации, лишь определенная часть M_избыт = (q) ^k (M_избыт < M_max), где:

n – длина кодовой комбинации,

k – число информационных символов.

Кодовые комбинации, которые используются для передачи полезной информации, называются разреженными, а остальные комбинации – запрещенными. Если под воздействием помех переданная (разрешенная) кодовая комбинация превращается в одну из запрещенных, то тем самым и обнаруживается наличие ошибок в принимаемой информации.

Ясно, что не все ошибки могут быть обнаружены, так как некоторая кодовая комбинация, под воздействием помех, может перейти в другую разрешенную комбинацию. Для указания исправлений и обнаруживающей способности корректирующих кодов ввели понятие расстояние Хэмминга.

Для двоичного кода расстояние Хэмминга (d_хэм) равно числу позиций, в которых кодовые слова не совпадают.

Например:

для кодов 100 и 111 d_хэм = 2;

для кодов 14320 и 14312 d_хэм = 2.

Если попарно сравнить все кодовые слова то, можно получить кодовое расстояние. Кодовым расстоянием ( d ) является минимальное расстояние Хэмминга.

Например:

min (d_хэм) = 3, тогда d = 3.

Для того чтобы код обнаруживал t ошибок, необходимо, чтобы кодовое расстояние d > t + 1, а исправлял d > 2 t + 1. Число t называется кратностью ошибки; оно равно числу позиций кодового слова, подвергающихся искажению под воздействием помех.

ЛИНЕЙНЫЕ КОДЫ

Среди всех кодов наиболее полно к настоящему времени изучены линейные коды. Эти коды называются также систематическими или групповыми. Рассмотрим эти определения подробнее.

Группой называется некоторое непустое множество элементов Г, для которых определена некоторая операция (сложения или умножения) и выполняются следующие аксиомы:

1. Если операция применена к двум элементам группы, то результат операции является также элементом группы, т.е. если a, b принадлежит Г, то a + b принадлежит Г для операции для операции сложения, и a ^. b принадлежит Г для операции умножения.

2. Для любых трех элементов группы а, Ь, с выполняется ассоциативный закон:

(a + b) + с = а + (b + с) – для операции сложения,

a ^. (b ^. c) = (a ^. b) ^. c – для операции умножения.

3. Существует нейтральный элемент. Если в качестве операции взято сложение, то нейтральный элемент называется нулем и удовлетворяет уравнению а + 0 = а. Если в качестве операции взято умножение, то нейтральный элемент называется единицей и удовлетворяет выражению a ^. 1 = а.

4. Каждый элемент группы обладает обратным элементом таким, что

а + (- а) = 0 для сложения,

a ^. a ^-1 = 1 для умножения.

Группа с операцией сложения называется аддитивной,а с операцией умножения - мультипликативной.

Некоторое подмножество элементов группы Г называется подгруппой Н, если оно удовлетворяет всем аксиомам группы.

Примеры группы:

- Совокупность всех действительных чисел без нуля образует группу, если в качестве операции взято умножение. Нейтральным элементом является 1, а обратным 1/ а.

- Совокупность всех действительных чисел образует группу, если в качестве операции взято обычное сложение. Нейтральным элементом является 0, а обратным элементом - этот же элемент с другим знаком.

Код называется групповым, если кодовые комбинации образуют некоторую подгруппу группы всех последовательностей длины n. Пусть, например, n = 7, т.е. имеется группа семиразрядных двоичных чисел. Среди этих чисел можно выделить следующие шестнадцать, которые удовлетворяют всем аксиомам группы, т.е. образуют подгруппу:

k n - k

0001 011

0010 110

0011 101

0100 111

0101 100

0110 001

0111 010

1000 101

1001 110

1011 000

1100 010

1101 001

1111 111

0000 000

Рассмотренный код позволяет передать шестнадцать различных сообщений. Из рассмотрения кодовых слов можно видеть, что минимальное расстояние Хемминга d_min = 3, т.е. код позволяет исправлять любую одиночную ошибку.

Если передаваемые сообщения представляют собой k – разрядные двоичные числа, то групповой код всегда может быть построен таким образом, что эти сообщения будут являться первыми к символами кода, как это сделано для рассмотренного выше примера. Код, построенный таким образом, называется систематическим кодоми обозначается (n; k) – код. Первое число в скобках показывает общее число символов в коде, второе – число информационных символов. Для нашего примера обозначение кода будет таким: (7; 4). Оставшиеся r = n - k символов называются проверочными. В групповых кодах проверочные символы образуются путем суммирования по модулю два символов, стоящих на-определенных позициях кодового слова. Поскольку операция суммирования по модулю два является линейной, то коды, образованные таким образом, называются линейными. Для рассмотренного примера правила образования проверочных символов будут следующие:

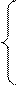a ₅ = a ₁ + a ₂ + a ₃

a ₆ = a ₂ + a ₃ + a ₄ (I)

a ₇ = a ₁ + a ₂ + a ₄

Поиск по сайту: