АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Мажоритарное декодирование линейных групповых кодов

Читайте также:
  1. Виды нелинейных регрессионных моделей, расчет их параметров
  2. Глава II. Решение системы линейных уравнений с использованием компьютерных приложений
  3. Графические модели и декодирование методом передачи сообщений
  4. Групповые водопроводы. Преимущества недостатки групповых водопроводов.
  5. Декодирование последовательности по алгоритму Витерби
  6. Декодирование сверточных кодов по максимуму правдоподобия. Алгоритм Витерби
  7. Декодирование эффективных кодов
  8. Дифференциальная импульсно-кодовая модуляция
  9. Збитки від повної загибелі судна завжди відшкодовуються без франшизи.
  10. Измерение неэлектрических и электрических величин с помощью ИП. Преобразователь линейных перемещений на дифракционных решетках.
  11. Интерпретация решения системы линейных уравнений
  12. Исследование эффективности циклических кодов

Этот способ декодирования привлекает как простотой описания, так и невысокой сложностью схемной реализации. Идея мажоритарного декодирования линейного кода базируется на системе проверочных равенств А именно, в кодах с мажоритарном декодированием каждый символ может быть выражен через другие символы несколькими способами. Это позволяет для определения истинного значения символа воспользоваться принципом большинства (мажоритарным принципом).

Рассмотрим построение мажоритарного декодера кода (6, 3).

Решим:

S 4= S 2 + S 3

S 5= S 1 + S 3

S 6= S 1 + S 2 + S 3

относительно S 1, S 2, S 3 и получим после присоединения тривиальных равенств S 1 = = S 1, S 2 = S 2, S 3 = S 3систему различных проверок:

 

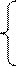
S 1 = S 3 + S 5 S 2 = S 3 + S4 S 3 = S 2 + S 4

S 1 = S 4 + S 6 S 2 = S 5 + S 6 S 3 = S 1 + S 5

S 1 = S 1 S 2 = S 2 S 3 = S 3

Для каждого из символов S 1, S 2, S 3 имеется по три независимых проверочных уравнения. При искажении одного символа искажается одно уравнение. Однако, поскольку решение принимается по большинству, то результат декодирования остается верным. В общем случае для исправления t ошибок код должен иметь не менее чем 2 t + 1 независимых проверочных уравнений. Для реализации принципа большинства используется мажоритарный элемент. Мажоритарный элемент на три входа реализует следующую функцию от трех переменных:

(а 1 а 2 а 3): f (а 1 а 2 а 3) = а 1 а 2 а 3 V а 1 а 2 а 3 V а 1 а 2 а 3 V а 1 a 2 а 3

 


Рис. 3. Схема мажоритарного декодера кода (6, 3)

Декодер для кода (6, 3) требует шесть сумматоров по модулю два (элемент исключающее или) и три мажоритарных элемента (М).

Пусть, ошибочен первый разряд, т.е. принятое слово, имеет вид (101 111). Схема мажоритарного декодера кода (6, 3), обеспечит получение на выходе декодера сигнала 0 0 1, который и передался в канал связи.

 

Список литературы

 

1. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. - М.: Мир, 1976.

2. Касами Т., Токура НгЙвадари Е., Йногаки. Теория кодирования.- М.: Мир, 1978.

3. Мак-Вильяме Ф.Дж., Слоэн Н.Дж. А. Теория кодов, исправляющих ошибки -М.: Связь, 1979.

4. Ахмед Н., Рао К.Р. Ортогональные преобразования при обработке цифровых сигналов.- М.: Связь, 1980.

5. Хэмминг Р.В. Теория кодирования и теория информации. - М.: Радио и связь. 1983.

6. Хетагуров Я.А., Руднев Ю.П. Повышение надежности цифровых устройств методами избыточного кодирования. - М.: Энергия, 1974.

7. Аршин М.Н., Садовский Л.Е. Коды и математика - М.: Мир 1983.

 


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)