Відокремлення коренів

Принципи розв’язання нелінійних рівнянь на ЕОМ

Процес розв’язання нелінійних рівнянь вигляду (4.1) або (4.2) на ЕОМ розбивається на два етапи:

1. відокремлення коренів;

2. уточнення коренів.

Перший етап іноді можна виконувати вручну, другий же виконується за допомогою спеціальних методів уточнення коренів та програм. Розглянемо особливості етапу відокремлення коренів.

Відокремлення коренів

Корінь рівняння , вважається відокремленим на відрізку , якщо на цьому відрізку дане рівняння не має інших коренів.

Відокремити корені – це означає розбити всю область допустимих значень 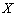(ОДЗ) на відрізки, в кожному з яких міститься один корінь (рис 4.2). Відокремлення коренів можна здійснити двома способами – графічним та аналітичним.

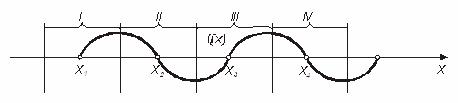
Рисунок 4.2 – Приклад розбиття ОДЗ на відрізки з єдиним коренем

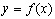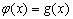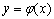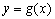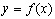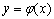Графічний метод. Будують графік функції для рівняння виду або представляють рівняння у вигляді та будують графіки функцій та . Значення дійсних коренів рівняння є абсцисами точок перетину графіка функції з віссю або абсцисами точок перетину графіків функцій та 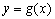. Відрізки, в яких знаходиться тільки по одному кореню, легко знаходяться наближено.

Приклад 4.1. Знайти наближено графічним способом корені рівняння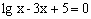

Розв’язок. Перепишемо рівняння наступним чином: 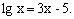Функції в лівій і правій частині рівняння мають спільну область визначення: інтервал 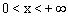. Тому будемо шукати корені саме на цьому інтервалі.

Будуємо графіки функцій 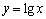і 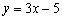(рис. 4.3).

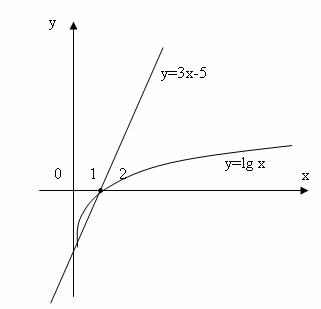
Рисунок 4.3 – Графічна інтерпретація прикладу 4.1

Для відокремлення коренів аналітичним методом можна рекомендувати наступний алгоритм:

1. Дослідити дане рівняння на монотонність і неперервність, визначити область допустимих та граничних значень.

2. Знайти – першу похідну, прирівняти її до нуля та знайти критичні точки.

3. Скласти таблицю знаків функції 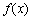, використовуючи для 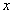значення критичних точок, граничних значень з ОДЗ і точок, отриманих на першому кроці при аналізі даного рівняння.

4. Визначити інтервали, на кінцях яких функція приймає значення протилежних знаків. Всередині цих інтервалів існує по одному і тільки одному кореню.

Поиск по сайту: