 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Алгоритм методу
1. На відрізку  вибираємо точку
вибираємо точку  , яка розділяє його на два рівних відрізки
, яка розділяє його на два рівних відрізки  і
і  , довжина яких рівна і знаходиться за формулою
, довжина яких рівна і знаходиться за формулою

2. Перевіряємо чи  , якщо так, то
, якщо так, то  – точний корінь початкового рівняння і переходимо до пункту 6.
– точний корінь початкового рівняння і переходимо до пункту 6.
3. У випадку, коли  , то з двох отриманих відрізків
, то з двох отриманих відрізків  і
і  вибираємо той, на кінцях якого функція
вибираємо той, на кінцях якого функція 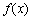 приймає значення протилежних знаків, тобто, якщо
приймає значення протилежних знаків, тобто, якщо 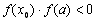 , тоді залишаємо відрізок
, тоді залишаємо відрізок  і точку
і точку  переносимо в точку
переносимо в точку  (
( ); якщо
); якщо  , то залишаємо відрізок
, то залишаємо відрізок  і переносимо точку
і переносимо точку  в точку
в точку  (
( ) і переходимо до пункту 1.
) і переходимо до пункту 1.
4. Процес ділення відрізка навпіл виконується доти, поки на якомусь етапі, або середина відрізка буде коренем, або буде виконана умова закінчення ітераційного процесу:  .
.
5. У цьому випадку за наближене значення кореня вибирають  .
.
6. Вивід результатів. Кінець алгоритму.
7. Відомо, що при цьому похибка не перевищує  , де
, де 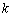 – число ітерацій.
– число ітерацій.
| Обчислення проводимо в табличній формі | ||||||||
| Припинимо обчисленя тоді, коли f(x)<e або |a-b|<e | ||||||||
| n | a | b | f(a) | f(b) | x=(a+b)/2 | f(x) | f(a)*f(x) | |a-b| |
| 3,1 | 3,5 | -7,527 | 6,125 | 3,300 | -1,489 | 11,208 | 0,400 | |
| 3,300 | 3,500 | -1,489 | 6,125 | 3,400 | 2,112 | -3,145 | 0,200 |
4.3.3 Метод Ньютона (метод дотичних)
Метод послідовних наближень, розроблений Ньютоном, дуже широко використовується при побудові ітераційних алгоритмів. Його популярність обумовлена тим, що на відміну від двох попередніх методів замість інтерполяції по двом значенням функції в методі Ньютона здійснюється екстраполяція за допомогою дотичної до кривої в одній точці.
Постановка задачі
Нехай корінь рівняння f(x)=0 відокремлений на відрізку  , на якому нелінійна функція f(x)монотонна і має різні знаки на кінцях відрізку, причому похідні
, на якому нелінійна функція f(x)монотонна і має різні знаки на кінцях відрізку, причому похідні  та
та  неперервні та зберігають постійні знаки на всьому відрізку
неперервні та зберігають постійні знаки на всьому відрізку  . Потрібно знайти наближене значення кореня
. Потрібно знайти наближене значення кореня  з заданою похибкою
з заданою похибкою  .
.
Геометричний зміст метода Ньютона полягає в тому, що дуга кривої  на відрізку
на відрізку  замінюється дотичною до цієї кривої, а наближене значення кореня визначається як точка перетину дотичної з віссю Ох, проведеної з одного з кінців досліджуваного відрізку. Рівняння дотичної має вигляд:
замінюється дотичною до цієї кривої, а наближене значення кореня визначається як точка перетину дотичної з віссю Ох, проведеної з одного з кінців досліджуваного відрізку. Рівняння дотичної має вигляд:
 .
.
Перший випадок. Нехай f(a)<0, f(b)>0, f¢(x)>0, f''(x)>0 (рис. 4.13, а) або f(a)>0, f(b)<0, f'(x)<0, f''(x)<0 (рис. 4.11, б). Проведемо дотичну до кривої  в точці B0(b; f(b)) і знайдемо абсцису точки перетину дотичної з віссю
в точці B0(b; f(b)) і знайдемо абсцису точки перетину дотичної з віссю  . Відомо, що рівняння дотичної в точці B0(b; f(b)) має вид: y-f(b)=f'(b) (x-b).
. Відомо, що рівняння дотичної в точці B0(b; f(b)) має вид: y-f(b)=f'(b) (x-b).
Припускаючи y=0, x=x1, отримаємо
 (4.8)
(4.8)
Тепер корінь рівняння знаходиться на відрізку [a, x1]. Застосовуючи знову метод Ньютона, проведемо дотичну до кривої в точці B1(x1; f(x1)) і отримаємо
 ,
,
і так далі (рис. 4.13).

Рисунок. 4.13 – Геометричний зміст методу Ньютона для випадків, коли
а) функція, яка досліджується, ввігнута (f'(x)>0, f''(x)>0)
б) функція, яка досліджується, опукла (f'(x)<0, f''(x)<0)
Даний процес ітераційний, тому формула для будь-якого n-го кроку ітерації має вигляд:
 . (4.9)
. (4.9)
В результаті отримана послідовність наближених значень x1, x2,..., xn,..., кожний наступний член якої ближчій до кореня  , ніж попередній. Однак всі xn залишаються більше істинного кореня
, ніж попередній. Однак всі xn залишаються більше істинного кореня  , тобто xn - наближене значення кореня
, тобто xn - наближене значення кореня  з надлишком. Процес визначення кореня продовжується багаторазово доти, поки не одержано наближений корінь із заданим степенем точності
з надлишком. Процес визначення кореня продовжується багаторазово доти, поки не одержано наближений корінь із заданим степенем точності
Другий випадок. Нехай f(a)<0, f(b)>0, f¢(x)>0, f¢¢(x)<0 (рис. 4.14, а) або f(a)>0, f(b)<0, f'(x)<0, f''(x)>0 (рис. 4.14).

Рисунок 4.14 –Геометричний зміст методу Ньютона для випадків, коли
а) функція, яка досліджується, опукла (f'(x)>0, f''(x)<0)
б) функція, яка досліджується, ввігнута (f'(x)<0, f''(x)>0)
Якщо провести дотичну до кривої  в точці B, то вона перетне вісь абсцис в точці, яка не належить відрізку
в точці B, то вона перетне вісь абсцис в точці, яка не належить відрізку  . Тому проведемо дотичну в точці А0(a; f(a)) і запишемо її рівняння для даного випадку: y - f(a) = f'(a) (x - a).
. Тому проведемо дотичну в точці А0(a; f(a)) і запишемо її рівняння для даного випадку: y - f(a) = f'(a) (x - a).
Припускаючи, що y = 0, x = x1, отримаємо
 (4.10)
(4.10)
Корінь x знаходиться тепер на відрізку [x1, b]. Застосовуючи знову метод Ньютона, проведемо дотичну до кривої в точці A1(x1; f(x1)) і отримаємо
 ,
,
і загалом  . (4.11)
. (4.11)
В результаті отримаємо послідовність наближених значень x1, x2,..., xn,..., кожний наступний член якої ближчій до істинного кореня x, ніж попередній, т.б. xn - наближене значення кореня x з недостачею.
Порівнюючи формули (4.10), (4.11) з раніше виведеними, (а також враховуючи випадки, які розглядаються на рисунках 4.14а,б помічаємо, що вони відрізняються одна від одної тільки вибором початкового наближення: в першому випадку за x0 приймався кінець b відрізка, в другому - кінець а.
При виборі початкового наближення кореня необхідно використовувати наступне правило: за початкову точку слід вибирати той кінець відрізка [a, b], в якому знак функції співпадає зі знаком другої похідної. В першому випадку f(b)×f''(x)>0 і початкова точка b=x0, в другому f(a)× f''(x)>0 і в якості початкового наближення беремо a=x0.
Для оцінки похибки можна користуватися загальною формулою
 , (4.12)
, (4.12)
де  (ця формула підходить і до метода хорд).
(ця формула підходить і до метода хорд).
В тому випадку, коли відрізок  настільки малий, що на ньому виконується умова М2<2m1, де M2
настільки малий, що на ньому виконується умова М2<2m1, де M2  , а
, а  , точність наближення на n -му кроці інтерполяційного процесу оцінюється наступним чином: якщо
, точність наближення на n -му кроці інтерполяційного процесу оцінюється наступним чином: якщо  .
.
Якщо похідна f'(x) мало змінюється на відрізку  , то для спрощення обчислень можна користуватися формулою
, то для спрощення обчислень можна користуватися формулою
 , (4.13)
, (4.13)
тобто значення похідної в початковій точці достатньо обчислити тільки один раз.
Процес побудови дотичної продовжується багаторазово доти, поки  , де
, де  – задана точність обчислень;
– задана точність обчислень;  – наближені значення кореня рівняння
– наближені значення кореня рівняння  , відповідно на
, відповідно на  та і - тому ітераційному кроці.
та і - тому ітераційному кроці.
| Обчислення проводимо в табличній формі | |||
| Припинимо обчисленя тоді, коли f(x)<e або |xi-xi-1|<e | |||
| n | a | f | f' |
| 1,400 | -0,2 | 11,8 | |
| 1,417 | 0,0040462 | 12,27889 |
· 4.3.5 Метод ітерацій (метод послідовних наближень)
Суть методу полягає у заміні початкового рівняння
 (4.18)
(4.18)
еквівалентним йому рівнянням
 , (4.19)
, (4.19)
Постановка задачі
Нехай задано рівняння  , де
, де 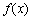 – неперервна нелінійна функція. Потрібно визначити корінь
– неперервна нелінійна функція. Потрібно визначити корінь  цього рівняння, який знаходиться на відрізку
цього рівняння, який знаходиться на відрізку  з заданою похибкою
з заданою похибкою  .
.
Виберемо довільним способом  і підставимо його в праву частину рівняння (4.18); тоді отримаємо
і підставимо його в праву частину рівняння (4.18); тоді отримаємо  . Потім це значення
. Потім це значення  підставимо знову в праву частину рівняння (4.19) і отримаємо
підставимо знову в праву частину рівняння (4.19) і отримаємо  (рис. 4.18 а,б). Повторюючи цей процес, отримаємо послідовність чисел
(рис. 4.18 а,б). Повторюючи цей процес, отримаємо послідовність чисел  . При цьому можливі два випадки:
. При цьому можливі два випадки:
· послідовність  збігається, тобто має границю, і тоді ця границя буде коренем рівняння (4.18).
збігається, тобто має границю, і тоді ця границя буде коренем рівняння (4.18).
· послідовність  розбігається, тобто не має границі.
розбігається, тобто не має границі.
Приведемо без доказу теорему, яка виражає умову, при якій ітераційний процес розв’язку нелінійного рівняння методом ітерацій на ЕОМ збігається.
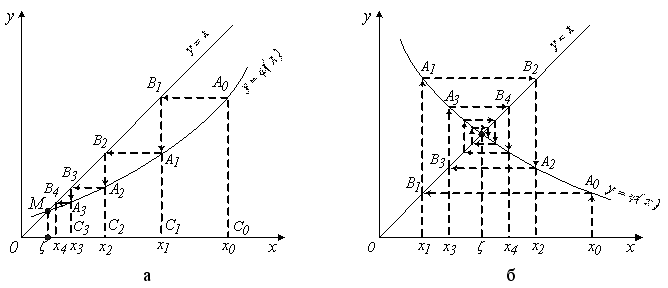
Рисунок 4.18 Геометрична інтерпретація методу ітерацій
Теорема. Нехай на відрізку  знаходиться єдиний корінь рівняння
знаходиться єдиний корінь рівняння  та у всіх точках цього відрізку похідна
та у всіх точках цього відрізку похідна  задовольняє нерівності
задовольняє нерівності  . Якщо при цьому виконується і умова
. Якщо при цьому виконується і умова  , то ітераційний процес збігається, а за нульове наближення
, то ітераційний процес збігається, а за нульове наближення  можна взяти число з відрізку
можна взяти число з відрізку  .
.
Розв’яжемо один етап ітерацій. Виходячи із заданого на попередньому кроці значення  , обчислюємо
, обчислюємо  . Якщо
. Якщо  , покладемо
, покладемо 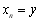 і виконаємо наступну ітерацію. Якщо ж
і виконаємо наступну ітерацію. Якщо ж  , то обчислення закінчують, за наближене значення кореня приймають величину
, то обчислення закінчують, за наближене значення кореня приймають величину 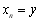 .
.
При використанні методу простих ітерацій основною операцією є вибір функції  в рівнянні
в рівнянні  , яку слід підібрати так, щоб
, яку слід підібрати так, щоб  і швидкість сходження послідовності
і швидкість сходження послідовності  до кореня
до кореня  тим вища, чим менше число
тим вища, чим менше число  .
.
Зведемо рівняння до виду x=f(x).
| Корінь рівняння знаходиться на відрізку | ||||||
| [ | 2,3 | , | 2,6 | |||
| f'(a)= | -0,14794 | f'(b)= | -0,091033 | |||
| Виконується умова |f'(x)| < 1 на всьому відрізку | ||||||
| Обчислення проводимо в табличній формі | ||||||
| Припинимо обчисленя тоді, коли |xi-f(xi)|<1 | ||||||
| n | x | fi(x) | |x-f(x)| | |||
| 2,4500 | 2,338887 | 0,111113 | ||||
| 2,3389 | 2,352968 | 0,014081 | ||||
4.3.2 Метод хорд
Метод хорд є одним з найбільш поширених методів розв’язання алгебраїчних і трансцендентних рівнянь. В літературі він також зустрічається під назвою "метод лінійного інтерполювання" і "метод пропорційних частин".
Постановка задачі
Розглянемо рівняння  , де
, де 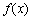 неперервна нелінійна функція, яка на відрізку
неперервна нелінійна функція, яка на відрізку  монотонна, диференційована і має єдиний корінь
монотонна, диференційована і має єдиний корінь  (тобто
(тобто  ). Потрібно знайти наближене значення кореня
). Потрібно знайти наближене значення кореня  з заданою похибкою
з заданою похибкою  .
.
Суть методу хорд полягає в тому, що на достатньо малому відрізку  дуга функції
дуга функції 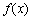 замінюється хордою ab, яка її стягує. За наближене значення кореня приймається точка х1 перетину хорди з віссю
замінюється хордою ab, яка її стягує. За наближене значення кореня приймається точка х1 перетину хорди з віссю  (рис.4.11.а).
(рис.4.11.а).

Рисунок 4.11 – Графічна інтерпретація методу хорд і процедури визначення рухомого кінця хорди
Рівняння хорди, яка проходить через точки має вигляд
 (4.4)
(4.4)
Знайдемо значення  , для якого
, для якого  , тобто для нерухомого кінця:
, тобто для нерухомого кінця:
 (4.5)
(4.5)
Ця формула називається формулою методу хорд. Тепер корінь  знаходиться всередині відрізка
знаходиться всередині відрізка  . Значення кореня
. Значення кореня  можна уточнити за допомогою метода хорд на відрізку
можна уточнити за допомогою метода хорд на відрізку  , тоді нове наближене значення кореня х2 знаходиться за формулою
, тоді нове наближене значення кореня х2 знаходиться за формулою
 .
.
Аналогічна для всякого  -го наближення до точного значення кореня
-го наближення до точного значення кореня  даного рівняння використовується формула:
даного рівняння використовується формула:
 (4.6)
(4.6)
Процес стягування хордою продовжується багаторазово доти, поки не одержано наближений корінь із заданим степенем точності
 (4.7)
(4.7)
де  – наближені значення коренів рівняння
– наближені значення коренів рівняння  , відповідно на
, відповідно на  і
і  -му ітераційному кроці;
-му ітераційному кроці;  – задана точність обчислень.
– задана точність обчислень.
Слід відмітити, що розглянутий випадок (рис.4.11.а) перетину функції 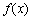 відрізку
відрізку  не є єдиним. Існує ще три варіанти перетину функції, кожний з яких відрізняється напрямком побудови хорд і відповідно рухомими кінцями відрізку. Наприклад, на рис.4.11.а,б рухомий кінець відрізку а, а на рис.4.11.в,г рухомий кінець –
не є єдиним. Існує ще три варіанти перетину функції, кожний з яких відрізняється напрямком побудови хорд і відповідно рухомими кінцями відрізку. Наприклад, на рис.4.11.а,б рухомий кінець відрізку а, а на рис.4.11.в,г рухомий кінець –  і відповідно формула 4.5 для нього має вигляд:
і відповідно формула 4.5 для нього має вигляд:

Для автоматизації цього алгоритму необхідно розробити правило для автоматичного вибору рухомого кінця хорди і відповідно формули для обчислення наближеного значення кореня. Існує два правила визначення рухомого кінця хорди.
Правило 1. Нерухомим кінцем відрізка є той, для якого знак функції співпадає із знаком другої похідної. Якщо  , то нерухомим є кінець
, то нерухомим є кінець  , а всі наближення до кореня
, а всі наближення до кореня  лежать зі сторони кінця
лежать зі сторони кінця  . Якщо
. Якщо  , то нерухомим є кінець
, то нерухомим є кінець  , а всі наближення до кореня
, а всі наближення до кореня  лежать зі сторони кінця
лежать зі сторони кінця  (рис.4.11.а,б,в,г).
(рис.4.11.а,б,в,г).
Правило 2. Якщо добуток першої на другу похідну функції 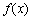 більший за нуль:
більший за нуль:  , то рухомий кінець
, то рухомий кінець  ; якщо добуток першої на другу похідну менший за нуль:
; якщо добуток першої на другу похідну менший за нуль:  , то рухомий кінець
, то рухомий кінець  .
.
http://posibnyky.vntu.edu.ua/chis_met/lek4.htm
Поиск по сайту: