 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Безызбыточные коды
|
Читайте также: |
КОДИРОВАНИЕ
 6.1 Основные понятия
6.1 Основные понятия
Каждое сообщение можно представить в виде комбинации символов, выбранных из заданного конечного множества, называемого алфавитом. Комбинация составляется по определенному закону — языку сообщений. Для передачи информации должны быть заданы алфавит и язык исходного сообщения.
Канал передачи имеет свой язык и алфавит. Язык канала задают исходя из требований дальности, помехоустойчивости, быстродействия, секретности и т. п. Алфавит канала определяется набором возможных физических состояний сигнала — например, положительной и отрицательной полярностью импульсов напряжения, импульсами тока различной частоты и др.
Для передачи информации алфавит и язык исходного сообщения необходимо поставить в соответствие алфавиту и языку канала. Процесс преобразования дискретного сообщения из одного языка в другой называют кодированием, а правило, по которому осуществляется это преобразование, — кодом. Общее число символов m, используемых для кодирования, называют основанием кода, а комбинации символов — кодовыми комбинациями. Число символов n, образующих кодовую комбинацию, называют ее длиной. В качестве символов используют цифры, буквы, арифметические или другие знаки. Так, при записи цифрами 1 и 0 (т. е. m = 2) кодовая комбинация при n = 5 может иметь вид, например, 10011.
Кодирование не изменяет количества информации, содержащегося в первоначальном сообщении. Однако при кодировании может меняться энтропия сообщения. Код с максимальной энтропией (т. е. с наименьшим числом символов для передачи данного количества информации) называют оптимальным. На практике не всегда возможно его использование. Выбор того или иного кода определяется характером и ответственностью передаваемой информации, характеристиками каналов передачи и рядом других причин.
Коды различают по основанию (двоичные и недвоичные), по длине кодовых комбинаций (с постоянной длиной — комплектные или равномерные и с различной длиной — неравномерные) и по другим признакам.
Наиболее общим критерием, определяющим многие свойства кода, является принцип комбинирования. При этом простые коды подразделяют на числовые и комбинаторные. Различают также коды с полным числом возможных комбинаций при данных m и n (коды на все сочетания, безызбыточные или первичные коды) и с частичным использованием комбинаций (избыточные), помехозащищенные и непомехозащищенные. Помехозащищенные коды подразделяют на коды с обнаружением ошибки и коды с исправлением ошибки. Под ошибкой понимают такие искажения, при которых один символ в кодовой комбинации замещается другим, принадлежащим к тому же алфавиту. Так, при двоичном алфавите под ошибкой понимают искажения типа 1 → 0 или 0 → 1.
При анализе помехоустойчивости кодов принимают, что канал связи задан, т. е. заданы скорость передачи и вероятности перехода (трансформации) символов друг в друга. Если вероятности перехода одинаковы, то канал связи называют симметричным. Если вероятность искажения отдельных символов больше, чем других, то канал называют несимметричным.
Ошибки в канале связи могут быть независимыми (некоррелированными, и зависимыми (коррелированными). В первом случае отдельные ошибки статистически не зависят друг от друга, во втором — каждая очередная ошибка статистически зависит от предыдущих. Зависимые ошибки могут возникать группами («пакетами»).
При независимых ошибках вероятность возникновения двух ошибок меньше, чем одной; трех — меньше, чем двух, и т. д. В симметричном канале вероятность ошибки подчиняется биномиальному закону распределения, т. е. быстро убывает с возрастанием кратности. Вероятность q -кратной ошибки  , где
, где 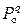 — вероятность ошибки в каждом отдельном символе. В первую очередь целесообразнее обнаруживать или исправлять ошибки наименьшей кратности как более вероятные.
— вероятность ошибки в каждом отдельном символе. В первую очередь целесообразнее обнаруживать или исправлять ошибки наименьшей кратности как более вероятные.
Безызбыточные коды
Числовые коды. Такие коды получили большое распространение в связи с развитием цифровых методов обработки информации. Они строятся по законам образования систем счисления. При этом основание кода соответствует основанию системы счисления m. Так, в десятичной системе m = 10, т. е. в ней используются 10 цифр — от 0 до 9. В двоичной системе m = 2 и соответственно имеются только две цифры — 0 и 1.
С помощью цифр записывается любое число. Место цифры в числе называют разрядом. Значение («вес») разряда определяется основанием m и порядковым номером разряда. При записи числа цифры располагают слева направо от высших разрядов к низшим. При этом каждое n -разрядное число N можно представить в виде:
 ,
,
где 0 ≤ Ki ≤ m – 1 цифра соответствующей системы счисления.
Например, десятичное число 1703 (m = 10, n = 4) можно записать  .
.
То же число в двоичной системе будет иметь вид: 
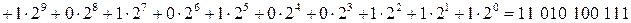 .
.
При записи чисел множитель mi опускают, так как положение цифры определяет ее вес. Числовые коды обычно записывают так же, как и числа в системах счисления. Общее число комбинаций в числовом коде N = mn.
Единичный код имеет один символ — 1 (единицу). Значение числа определяется количеством единиц. Так, числу 1 соответствует кодовая комбинация 1, числу 2 — комбинация 11, числу 3 — 111 и т. д. Код некомплектный, так как число элементов в комбинациях неодинаково. Добавление или подавление помехой одного элемента приводит к ошибке, наличие которой невозможно обнаружить. Несколько увеличить помехозащищенность кода можно, дополнив его до некоторого постоянного числа символов нулями (т. е. сделав его комплектным) и обеспечив контроль по числу элементов в кодовой комбинации. При этом данный код становится вариантом избыточного двоичного кода с низкой помехозащищенностью (ошибки типа 0 → 1 и 1 → 0 не обнаруживаются).
Двоичный код наиболее широко применяется в технике, так как он соответствует двоичной природе многих событий и явлений. Операции с двоичными числами достаточно просты. Число возможных комбинаций N =2 n. Ряд двоичных чисел представлен в табл.6.1.
Двоичные коды машинных слов ЭВМ содержат до 32 разрядов. Запись их довольно громоздка и ненаглядна, что может приводить к ошибкам. Поэтому часто пользуются записью двоичного кода в восьмеричной или шестнадцатеричной системе счисления, вторая является наиболее короткой и удобной. При этом безызбыточные комбинации двоичного кода разбивают на четырехразрядные группы — тетрады. Каждую из них обозначают соответствующей шестнадцатеричной цифрой. Например, двоичная комбинация 1001 1000 1101 1111 в шестнадцатеричной системе записи примет вид: 9 8 DF.
Таблица 6.1
| Десятичное число | Двоичное четырехразрядное число | Форма записи шестнадца-теричного числа | Комбинация кода Грея, соответствующая десятичному числу | Десятичное число | Двоичное четырехразрядное число | Форма записи шестнадца-теричного числа | Комбинация кода Грея, соответствующая десятичному числу |
| A | |||||||
| B | |||||||
| C | |||||||
| D | |||||||
| E | |||||||
| F |
Нечисловые двоичные коды. Известны двоичные коды, в которых «вес» цифры в разряде в различных комбинациях не остается постоянным. К ним относятся, например код Грея и оптимальный код Шеннона-Фано.
В коде Грея две соседние комбинации отличаются не более чем в одном разряде. Код Грея выполняется в соответствии с правилом: если в комбинации безызбыточного двоичного кода в старшем разряде по отношению к рассматриваемому стоит 0, то при переходе к коду Грея его символ сохраняется; если же стоит 1 — меняется на обратный. Пусть, например, дана комбинация двоичного кода 01001. Преобразуем ее в комбинацию кода Грея. В младшем разряде двоичного числа — 1, во втором — 0. Поэтому в коде Грея сохраняется символ 1. В следующем разряде двоичного кода стоит также 0, соответственно в коде Грея запишем 0. В четвертом разряде двоичного кода находится 1, поэтому в коде Грея изменим символ на 1. Следующий символ сохраняет значение. Таким образом получаем комбинацию 1101.
Наиболее часто код Грея применяют в датчиках, преобразующих угол поворота в код, для чего используют кодирующую маску — диск, содержащий секторы по числу комбинаций.
Каждый сектор условно разделен на части, число которых равно числу разрядов. Если в разряде комбинации имеется I, то в соответствующей части сектора пробивается отверстие. Установив с разных сторон такой маски источник света и фотоприемник, можно угол поворота диска преобразовать в код. При считывании информации, когда диск находится на границе перехода от одной комбинации в другую, при использовании простого двоичного кода возможны большие погрешности за счет того, что вследствие незначительных неточностей в изготовлении одна часть считанных разрядов будет принадлежать одной комбинации, а другая часть — смежной комбинации. Так, при переходе от числа 3 (011) к числу 4 (100) могут быть получены комбинации двоичного кода 000, 111 и др. В коде Грея при переходе к смежной комбинации меняется только один элемент: числу 3 соответствует комбинация 0010, числу 4— 0110. Поэтому на границе между комбинациями будет передаваться или то, или другое число. Таким образом дополнительно ошибки по отношению к ошибке квантования не возникает.
Код Шеннона-Фано — это неравномерный код. При его построении учитывается вероятность появления определенных сообщений (или соответствующих им комбинаций). Тем сообщениям, вероятность которых велика, приписываются кодовые комбинации с малым числом элементов. Сообщениям с малой вероятностью приписываются комбинации с большим числом символов:
| Номер сообщения | ||||||||
| Вероятность сообщения…… | 0,22 | 0,2 | 0,18 | 0,15 | 0,1 | 0,08 | 0,05 | 0,02 |
| Кодовая комбинация… |
При построении кода все сообщения вписывают в порядке убывания. Далее все сообщения делят на две группы с примерно равными вероятностями появления комбинаций из этих групп.
Так, в рассмотренном примере в одну группу войдут сообщения 1 и 2, в другую 3—8. В кодовой комбинации сообщений в старший разряд первой группы записывают 0, а в старший разряд второй группы — 1. Далее каждая группа вновь делится на две части и по тому же правилу в кодовые комбинации полученных подгрупп записывают второй элемент: 0 — в нечетные подгруппы, 1 — в четные и т. д.
Такой код называют оптимальным, так как в нем на передачу длинных сообщений (в которых много раз повторяются различные комбинации) затрачивается минимально возможное число импульсов, а следовательно, и время. Близок к оптимальному код Морзе, в котором также наиболее короткие комбинации приписываются наиболее часто встречающимся буквам алфавита.
Составные коды. Эти коды основаны на использовании двух и более различных законов образования. К ним относится широко распространенный двоично-десятичный код. Он принадлежит к группе кодов, которые благодаря двоичному характеру символов (или сигналов) позволяют осуществить легкий переход к десятичной системе. В этом коде каждая цифра от 0 до 9 десятичного числа записывается четырехразрядным двоичным числом. При этом возможно N = 24 = 16 различных комбинаций. Для обозначения 10 цифр служат 10 из них. В принципе можно использовать любые комбинации из 16. Наибольшее применение нашел двоично-десятичный код, в котором десятичные цифры обозначаются соответствующими им комбинациями натурального ряда двоичных чисел. Такой код называют кодом типа 8, 4, 2, 1 — по весу разрядов в двоичном числе. Например, число 325 запишется следующим образом: 0011—0010—0101. Передача разделительных знаков между тетрадами при комплектном коде не обязательна, так как каждый разряд содержит одинаковое число символов.
Возможны и другие виды двоично-десятичных кодов, например, 2, 4, 2, 1:
| Десятичная цифра………. | ||||||||||
| Код 2, 4, 2, 1 |
При этом число 325 запишется в виде: 0011—0010—1011. Цифры 9, 8, 7, 6 и 5 записываются в инверсном виде по отношению к цифрам 0, 1, 2, 3 и 4. Код позволяет упростить двоично-десятичные счетчики за счет суммирующего счетчика, который до четвертого импульса работает обычным образом. На пятом импульсе все его триггеры переключаются обратно и далее он вновь работает, как обычный суммирующий счетчик.
Коды, применяемые в телеграфии и при передаче данных. Код Морзе служит для передачи сообщений вручную. Перед вручением адресату сообщение необходимо дешифрировать. Автоматическая дешифрация и защита от искажений неравномерных кодов сложны. Поэтому были разработаны комплектные телеграфные коды, из которых широко применяют пятиэлементный код Бодо. Весь алфавит в этом коде разделен на четыре группы по семь букв (символов). Код группы — двухразрядный: 00, 10, 01, 11. Внутри каждой группы символы кодируются трехразрядными двоичными числами: 100, 010, 001, 110, 101, 011, 111. Аналогично тем же комбинациям кодируются цифры и другие символы (точки, запятые, двоеточия и др.). Для передачи буквенного текста передается код буквы (00001) и затем — пятиразрядные комбинации кода текста; перед передачей цифр или других символов передается код цифры (00010).
На базе кода Бодо в различных странах разработаны телеграфные равномерные коды. Различие в кодах затрудняло международные телеграфные связи, поэтому в 1931 г. Международный консультативный комитет по телеграфии (МККТ) принял стандартный код МТК-1, близкий по виду к коду Бодо. Для стартстопных телеграфных аппаратов с клавиатурой пишущей машинки в 1932 г. был принят код МТК-2. В состав кода вошли 32 информационных и служебных символа. Он отличается от кода Бодо лучшей приспособленностью к пользованию клавиатурой пишущих машинок при передаче русского и латинского текстов. Этот код с незначительными изменениями применялся для обмена информацией в первых образцах ЭВМ.
Для передачи данных с использованием ЭВМ разработан ряд стандартных кодов, обеспечивающих кодовую совместимость ЭВМ. Структурной единицей при передаче данных принята восьмибитная комбинация — байт.
Так, в ЕС ЭВМ используются коды — КОИ-7, КОИ-8 (для обмена данными), КПК-12 — для перфокарт и ДКОИ — для внутренних операций в машинах.
Код КОИ-7 содержит 128 символов международного алфавитно-цифрового набора, включая математические и специальные символы. В этом коде символы кодируются таким образом. Кодовая комбинация состоит из двух частей: три старших разряда а 7, а 6 и а 5 соответствуют адресу столбца, а четыре младших — а 4 — а 1 — адресу строки кодовой таблицы, в которой размещены кодируемые символы. Адрес, т. е. номера строк и столбцов, записывают в двоичном неизбыточном коде. Например, цифре 1 соответствуют комбинация 011 0001, символу % — 010 0101, букве К — 100 1011 и т. п. Код имеет три модификации, позволяющие иметь дополнительные управляющие символы (например, ВХ (000 1111) — обозначающий передачу латинских букв, ВЫХ (1000 1110) — русских букв). Восьмой бит используется как контрольный (для защиты от искажений по четности).
Код КОИ-8 объединяет все модификации КОИ-7. Для определения модификации используют дополнительный восьмой разряд.
Код для обработки информации ДКОИ содержит 256 кодовых комбинаций, включающих ряд функциональных, в том числе ряд комбинаций, предназначенных для кодирования тех или иных функций (16 столбцов и 16 строк, пронумерованных в шестнадцатеричной системе). Он разработан на основе международного кода EBCDIC (Exended Binary Decimal International Code) с добавлением букв русского алфавита. Например, кодовая комбинация 1110 0111 соответствует символу «=», кодовая комбинация 1111 0110 —символу «?» и т. д.
Использование того ли иного кода определяется протоколом обмена данными, согласовываемым при разработке систем.
Комбинаторные коды. Такие коды основаны на применении математической теории соединений: перестановок (Рn), размещений (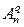 ) и сочетаний (
) и сочетаний ( ).
).
Коды, построенные по закону перестановок, содержат n символов в каждой комбинации. Отдельные комбинации отличаются одна от другой только порядком следования символов. Общее число возможных комбинаций  . Так, при трех символах а, б и в возможны следующие перестановки: абв, авб, бав, бва, ваб, вба.
. Так, при трех символах а, б и в возможны следующие перестановки: абв, авб, бав, бва, ваб, вба.
Коды по закону размещений представляют собой комбинации из n элементов по q символов, отличающихся символами или порядком их следования. Число возможных комбинаций
 .
.
Так, при n = 3 (например, а, б, в) и q = 2 возможны комбинации: аб, ав, ба, бв, ва, вб.
Коды по закону сочетаний представляют собой комбинации по q символов из n возможных, отличающиеся только символами. Число комбинаций
 .
.
Так, при n = 4 (например, а, б, в и д) возможны сочетания: аб, ав, ад, бв, бд и вд. Такие коды называют кодами на одно сочетание (в каждой комбинации одинаковое число элементов). Если из заданного числа элементов составить комбинацию сочетаний по 1, по 2,..., по n элементов, то общее число комбинаций  ; такой код называют кодом на все сочетания. Код типа
; такой код называют кодом на все сочетания. Код типа  при временном разделении элементов сигналов часто называют распределительным.
при временном разделении элементов сигналов часто называют распределительным.
Поиск по сайту: