 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Помехозащищенные коды
|
Читайте также: |
Принципы построения помехозащищенных кодов. Простые числовые комплектные коды при числе символов m и числе элементов n 0 позволяют образовать 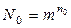 комбинаций. Отсюда минимальная длина кодовой комбинации, необходимая для образования всех N 0 комбинаций,
комбинаций. Отсюда минимальная длина кодовой комбинации, необходимая для образования всех N 0 комбинаций,
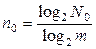 .
.
Коды, в которых используется совокупность всех комбинаций минимальной длины, называют минимальными или кодами безызбыточности. Их отдельные комбинации могут отличаться друг от друга всего в одном элементе. Искажение какого-либо одного элемента в результате воздействия помехи приводит к изменению передаваемой комбинации и, следовательно, к ошибке. Для оценки помехозащищенности пользуются кодовым расстоянием d — числом разрядов, в которых элементы одной кодовой комбинации отличаются от другой. Кодовое расстояние может быть определено сложением обеих комбинаций по модулю 2 (mod 2) так, как это показано в табл. 6.2 (сложение по mod 2 обозначают знаком  ).
).
В сумме комбинаций будут нули в тех разрядах, где символы в обеих комбинациях одинаковы, а единицы — где символы различные. Расстояние между различными кодовыми комбинациями из заданного набора наглядно иллюстрируется матрицей кодовых расстояний. Пусть, например, дан некоторый произвольный набор комбинаций: 1) 1000; 2) 1100; 3) 0101; 4) 1111. Определим, например, кодовое расстояние между каждой парой комбинаций в некотором их произвольном наборе (табл. 6.3).
Кодовое расстояние между комбинациями 1 и 2 равно 1, между комбинациями 2 и 3 равно 2 и т. д. В первом случае комбинации могут переходить одна в другую уже при одиночной ошибке, во втором — минимум при тройной. Для повышения помехозащищенности кода необходимо увеличивать минимальное кодовое расстояние d min.
Существуют два основных подхода к формированию помехозащищенного кода: выбор из заданного набора (множества) безызбыточного кода комбинаций (слов) помехозащищенного кода с заданными свойствами; непосредственное преобразование k -значных комбинаций безызбыточного кода в (n > k)-значную комбинацию помехозащищенного кода с заданными свойствами.
Таблица 6.2 Таблица 6.3
| x | y | x  y y
| Номер кодовой комбинации | Кодовые расстояния между комбинациями | ||||
| – | ||||||||
| – | – | |||||||
| – | – | – |
В обоих случаях длина слов помехозащищенного кода оказывается большей, чем у безызбыточного кода с таким же набором комбинаций. Поэтому такие коды называют кодами с избыточностью. Пусть у безызбыточного кода длина кодового слова n 0, тогда у избыточного кода она больше: n = n 0 + D n. При сравнении кодов избыточность оценивают коэффициентом избыточности R:
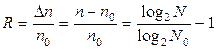 .
.
Коды с обнаружением и исправлением ошибок. Чтобы обнаружить ошибку, возникающую в одном символе, достаточно увеличить минимальное кодовое расстояние до d min = 2. При этом декодирующее устройство будет реагировать только на заданный набор комбинаций, запрещая исполнение всех других, отличающихся от них по крайней мере на единицу. Для обнаружения одновременной ошибки в двух элементах кода кодовое расстояние должно быть увеличено до d min = 3, в трех элементах до d min = 4 и т. д. Таким образом, для обнаружения ошибок кратностью sоб нужно иметь минимальное кодовое расстояние d min ≥ sоб + 1. При d > 2 можно не только обнаруживать, но и исправлять ошибки. Способность кода обнаруживать и исправлять ошибки определяется минимальным кодовым расстоянием d = sи + sоб + 1, где sи — число исправляемых ошибок (sи ≤ sоб). Если исправляются все обнаруженные ошибки, то d = 2sи + 1. Отсюда для исправления одиночной ошибки d min = 3.
Среди помехоустойчивых кодов различают блочные и непрерывные.
К блочным относятся коды, с помощью которых сообщения передаются блоками из некоторого конечного числа символов. Из них равномерные коды имеют постоянное число символов в комбинации (например, код Бодо), неравномерные — различное (например, код Морзе). Непрерывные коды являются непрерывной последовательностью информационных и проверочных разрядов. Места этих разрядов определяются рекуррентными выражениями. Четкое разделение кодовых комбинаций отсутствует. Блочные коды могут быть разделимыми и неразделимыми. У разделимых кодов разряды четко делятся на информационные и проверочные, причем места проверочных разрядов в кодовой комбинации строго определены. У неразделимых, например у равновесного кода, такого деления нет.
Разделимые коды включают две группы: систематические и несистематические. К систематическим относятся коды, у которых сумма по модулю 2 двух разрешенных комбинаций является комбинацией того же кода. Их примером являются коды Хэминга и циклические коды. К несистематическим кодам относятся код, в котором проверочная комбинация является суммой единиц в информационной части, и код с проверкой на четность.
Если при формировании помехозащищенного кода ставится только задача получения d min, то наиболее общим является табличный метод. В головку таблицы выписывают комбинации исходного безызбыточного кода. В левый столбец записывают комбинации ошибок для каждого кодового расстояния. Под каждой комбинацией исходного кода записывают искаженные комбинации, возникающие при одиночной, двойной и других ошибках. Первую комбинацию в исходном коде выбирают произвольно. Затем вычеркивают комбинации, в которые первая переходит при числе искажений, равном заданному или меньше его. Из оставшихся невычеркнутых комбинаций произвольно выбирают еще одну; вновь из оставшихся вычеркивают комбинации, отстоящие на d min — 1, и т. д.
Например, возьмем в качестве исходного двоичный код с n = 3 (табл. 6.4). Пусть надо выбрать кодовые комбинации с d min = 2 (тогда d = d min — 1 = 1).
В качестве первой комбинации выбираем 001 (очередность выбора комбинации обозначена цифрой над ней: 0011 — первая).
В исходном коде вычеркиваем комбинации, расположенные в столбце ниже выбранной (000, 011 и 101). Выбираем следующую комбинацию 010 и дополнительно к уже вычеркнутым 000 и 011 исключаем комбинации 110 (вычеркнутые комбинации обозначены знаком *). Остаются не исключенными комбинации 100 и 111. Таким образом, выбранный набор 001, 010, 100, 111.
Нетрудно убедиться, что между оставшимися комбинациями d mln= 2. Аналогично можно построить код с d mln = 3, если учесть двойные ошибки, и с любым другим d mln.
Практически такой метод можно реализовать только при относительно небольшом числе разрядов, иначе таблица будет очень громоздкой. При значительном числе разрядов комбинацию можно выбрать с помощью вычислительной машины. Недостатком рассмотренного метода является также произвольный выбор первой и последующих комбинаций.
Коды с обнаружением ошибок. В телемеханике используют коды с проверкой на четность, двоичный код на одно сочетание, код с повторением и др.
Таблица 6.4
| Комбинации ошибок | Искаженные комбинации при исходном коде | |||||||
| 0011 | 0102 | 011* | 1003 | 101* | 110* | 1114 | ||
| d = 1 | ||||||||
| d = 2 | ||||||||
| … | … | … | … | … | … | |||
| … | … | … | … | … |
Код с проверкой на четность может быть получен двумя способами. Первый способ представляет собой вариант табличного метода и состоит в том, что все комбинации двоичного кода разбиваются на две группы, в одну из которых входят комбинации с четным, а в другую — с нечетным числом единиц:
| Комбинации с четным числом единиц | ||||
| То же с нечетным числом единиц |
Для передачи сообщений используют комбинации первой или второй группы.
Код может быть получен с помощью линейных математических преобразований (второй способ). Все элементы исходной кодовой комбинации по mod 2 суммируются. Если сумма равна 1, то для получения четных комбинаций к исходной добавляется еще единица; если же сумма равна 0, то добавляется 0 (для получения нечетных комбинаций делается наоборот). Пример такого кода приведен в табл. 6.5.
Таблица 6.5
| Исходная комбинация | Сумма элементов по модулю 2 | Полученная комбинация |
1 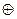 1 1  1=1 1=1
| ||
1  1 1  1=0 1=0
|
Код имеет d min = 2, он может обнаружить любое одиночное искажение, а также все искажения нечетной кратности.
Избыточность кода
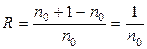 .
.
Двоичный код на одно сочетание выполняется выбором из двоичного кода на все сочетания комбинаций с одинаковым числом единиц (l). Такой код также называют равновесным: 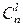 . Например, код
. Например, код 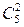
| 1) 11000 | 3) 10010 | 5) 01100 | 7) 01001 | 9) 00101 |
| 2) 10100 | 4) 10001 | 6) 01010 | 8) 00110 | 10) 00011 |
Избыточность кода
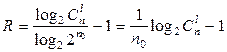 .
.
Код обнаруживает любые одиночные искажения, а также многие двойные, тройные и другие искажения.
Коды с повторением предусматривают повторение каждой комбинации 2 раза или более. Такие коды могут быть в двух вариантах: повторение без инверсии и повторение с инверсией. Повторяться могут целые комбинации или отдельные элементы. Например, комбинация 01100 в таких кодах представляется таким образом:
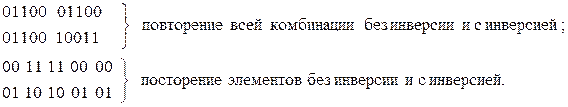
Число элементов n и кодовое расстояние d увеличиваются пропорционально кратности повторения g:
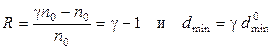
где 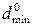 — минимальное кодовое расстояние в исходном коде.
— минимальное кодовое расстояние в исходном коде.
При двукратном повторении безызбыточного кода обнаруживаются все одиночные искажения, все ошибки нечетной кратности и многие другие. Код с повторением и с инверсией более целесообразен при несимметричном канале, в котором чаще появляются ошибки одного знака.
Линейные коды
В устройствах передачи информации широко распространены линейные коды, способные обнаруживать и исправлять ошибки. Они состоят из информационных и проверочных символов и являются разделимыми. Проверочные символы представляют собой различные линейные комбинации информационных символов. При декодировании проверяются линейные соотношения между символами.
Групповые коды. Для двоичных кодов в качестве линейной операции принято посимвольное сложение по модулю 2. Коды, построенные таким образом, называют групповыми, так как они образуют алгебраическую группу по отношению к этой операции (группой называется множество элементов с одной алгебраической операцией: сложение или умножение и т. д.). Каждая кодовая комбинация при этом является суммой по модулю 2 некоторых двух других кодовых комбинаций.
Групповые коды обозначают n, k, d, где n — общее число разрядов; k — число информационных разрядов; d — кодовое расстояние. Наиболее распространен способ задания таких кодов с помощью таблиц — «порождающих» или «базисных» матриц с числом строк k и рядов n. Например, для кода 7, 4, 3 «порождающие» матрицы G имеют вид:
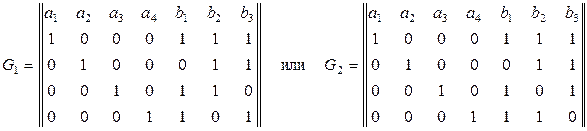
Матрица может быть составлена из любого набора кодовых векторов при условии, что сумма по модулю 2 любых сочетаний векторов не равняется нулевому вектору. При этом те или иные кодовые комбинации из общего числа 2 k могут быть получены суммированием по модулю 2 различных сочетаний строк порождающей матрицы.
Первые k рядов матрицы (a l, a 2,..., ak) представляют собой информационную часть. При синтезе кода с различными n и k она может быть записана в так называемой канонической форме в виде единичной матрицы («1» по диагонали). Проверочная часть (контрольная подматрица Ь 1, Ь 2,..., bn - k) формируется различными способами со следующими ограничениями: каждая строка контрольной подматрицы содержит не менее d — 1 единиц; строки контрольной подматрицы отличаются не менее чем в d — 2 позициях; сумма любых d — 1 строк не равна нулю.
Таким образом, для каждого n, k, d кода может быть получено то или иное число вариантов. Все варианты эквивалентны по вероятности правильного приема, но могут иметь различные по степени сложности кодирующие и декодирующие устройства.
Правильность принятого кода определяется z = n — k проверками, которые сводятся к контролю четности суммированием по модулю 2 соответствующих проверочных и информационных символов. В результате проверок получают двоичное число S l, S 2,..., Sn - k, называемое проверочным вектором, или синдромом. Здесь S l — результат первой проверки; S 2 — второй; Sn - k — результат z -й проверки. Если синдром равен нулю, то это свидетельствует об отсутствии ошибки, а если не равен нулю, — то ошибка есть. По виду синдрома ошибка может быть только обнаружена или обнаружена и исправлена.
Один из методов обнаружения ошибки рассмотрим на примере кода Хэминга (n, k, d = 3), сущность которого в том, что в результате z проверок получают двоичное число, которое при переводе в десятичное говорит о номере позиции, в которой произошла ошибка. Для этого синдром Sz, Sz -1,..., S 2, S 1 должен иметь число двоичных разрядов z, соответствующее десятичному числу n — 1 (от 0 до n -й позиции кода). Следовательно, при z проверочных разрядах:
 ; (6.1)
; (6.1)
 . (6.2)
. (6.2)
Знак «>» в выражении (6.1) говорит о том, что z округляется до целого числа в большую сторону. Из выражений (6.1) и (6.2) следует, что максимальное число информационных разрядов k при заданном n будет в случае, если n + 1 = 2 с, где с — целое число.
Число информационных символов для N сообщений определяется из условия k ≥ log2 N. Зная k и соотношение между z и n, можно определить число контрольных символов:
| k …… | ||||||||||||
| z …… | ||||||||||||
| n …… |
Контрольными символами, формируемыми кодирующим устройством, дополняют соответствующие последовательности символов до четного числа единиц с таким расчетом, чтобы при безошибочном приеме S l, S 2,..., Sz равнялись нулю. Для упрощения кодирующего устройства в качестве контрольных символов удобнее выбрать такие, которые встречаются в последовательностях S l, S 2,..., Sz только один раз. При этом символ проверочного разряда может быть найден в результате решения только одного уравнения. Как видим, в выражения (6.3) — (6.6) для Si один раз входят те разряды, номер которых равняется 2 с. Именно их (a 1, a 2, a 4, а 8) и выбирают в качестве контрольных, приняв в них Sl, S2,... = 0; найдем значения контрольных символов:
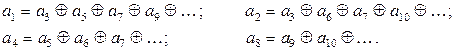
В качестве примера рассмотрим процесс передачи и приема одной из комбинаций кода 7, 4, 3. Пусть была передана комбинация
| а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 | . |
Проверочные позиции (контрольные символы): а 1 = 0, при приеме кодовой комбинации осуществляют z проверок. Первая проверка должна дать S 1 — младший разряд синдрома. Если S 1 = 1, то это значит, что ошибка произошла в одном из символов, находящемся на позициях 1, 3, 5, 7,..., т. е. на позициях, номер которых имеет в двоичной системе единицу в младшем разряде. Таким образом
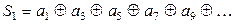 . (6.3)
. (6.3)
Второй проверке подвергаются разряды, номер которых в двоичной системе имеет единицу во втором разряде:
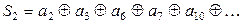 . (6.4)
. (6.4)
Аналогично
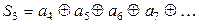 . (6.5)
. (6.5)
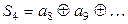 . (6.6)
. (6.6)
а 2 = 1, а 4 = 1. Допустим, что в результате искажения на приемной стороне принята комбинация 0101110 (искажение на пятой позиции). Тогда
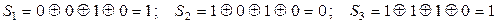 .
.
Полученный синдром S 3 S 2 S 1 → 101 (пять в десятичной системе, и следовательно, ошибочно принят пятый элемент комбинации а 5). Исправив его (с 1 на 0), окончательно получим 0101010.
Пусть искажение произошло в проверочном разряде, например, в а 4. Тогда будет принята комбинация 010010. При этом S 1 = 0; S 2 = 0; S 3 = 1, т. е. S 3 S 2 S 1 → 100, а значит, искажен символ а 4. Коррекция в этом случае не нужна, так как комбинация исходного кода принята правильно.
Циклические коды — это линейные коды, у которых любая кодовая комбинация anan -1 an -2... a 2 a 1 при циклическом сдвиге дает кодовую комбинацию an -1 an -2... a 2 a 1 an, принадлежащую тому же коду.
Синтез циклических кодов осуществляют алгебраическими методами, отображая кодовые комбинации полиномами. При этом цифры разрядов двоичного кода рассматривают, как коэффициенты при переменной х. Например 100101 ® 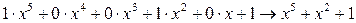 .
.
Для получения циклического кода сначала выбирают безызбыточный двоичный код, число разрядов k в комбинациях которого обеспечивает передачу заданного объема сообщений (2 k). Этому коду соответствует полином G (х) степени (k — 1). Например, кодовая комбинация 1111 отображается полиномом G (х) = х 3 + х 2 + х + 1. При этом полный объем сообщений будет содержать 24 = 16 кодовых комбинаций (включая комбинацию 0000).
Длина комбинации помехозащищенного кода должна содержать большее число разрядов n = k + r, где r — число проверочных символов.
Известны различные способы формирования циклических кодов. Рассмотрим один из них, при котором в сформированных комбинациях коэффициенты при высших степенях полинома (от n до n — k) соответствуют информационным разрядам, а при низших (n — k — 1 и ниже) — проверочным.
Чтобы получить полином, соответствующий n -разрядному коду, исходный G (х) умножают на хr.
Для дальнейших операций с кодом с целью обеспечения его защиты от помех используют так называемый «порождающий» полином. Его находят разложением на множители двучлена хn — 1 = P 1(x) · P 2(x) ·... · Рi (х).
В качестве порождающего полинома выбирают сомножитель РS (х), имеющий степень r ≤ n — k. При таком полиноме для формирования кодовых комбинаций циклический код при r ≥ 2 будет обнаруживать все одиночные и двойные ошибки, а также все групповые ошибки с числом искаженных символов r и менее. Порождающий полином вида PS (x) = 1 + х позволяет обнаружить все одиночные и любое число нечетных ошибок.
Из всех ошибок длиной r + 1 разрядов не обнаруживается 1/2 r– 1 часть, а при длине большей, чем r + 1, 1/2 r часть.
Для получения помехозащищенной кодовой комбинации F (х) произведение G (х) хr делят на PS (x). Остаток от деления R (х) суммируют с произведением G (х) хr: F (х) = G (х) хr + R (х). Полученная комбинация делится на полином PS (x) без остатка.
Операции, необходимые для получения помехозащищенного кода, выполняются соответствующими аппаратными или программными средствами.
Рассмотрим пример формирования помехозащищенного кода на основе безызбыточного четырехразрядного кода. Пусть исходная комбинация отображается полиномом G (х) = х 3 + х 2 + х + 1, число проверочных символов r = 3.
Умножив G (х) на х 3, получим (х 3 + x 2 + х + 1) х 3 = х 6 + х 5 + х 4 + х 3 → 1111000. Первые четыре символа представляют собой исходную комбинацию, а три последних предназначены для контрольных символов. Для выбора порождающего полинома разложим двучлен хn — 1 = х 6 — 1 на сомножители х 6 — 1 = (х 3 + 1)·(х 3 — 1). В качестве порождающего полинома выберем х 3 + 1 ↔ 1001. Разделив полином х 6 + х 5 + + х 4 + х 3 на х 3 + 1, найдем, что остаток от деления R (х) = х 2 + х. Тогда кодовая комбинация для передачи по линии связи примет вид:
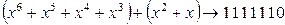 .
.
Кодовые комбинации также принимаются с помощью деления на порождающий полином. При отсутствии ошибки принятая комбинация F' (х) делится на него без остатка. Наличие остатка говорит об ошибке F' (х) = F (х) + + Е (х), где Е (х) — полином ошибки.
При соответствующем выборе порождающего полинома по величине Е (х) можно не только обнаружить ошибку, но и скорректировать ее.
6.5 Методы повышения достоверности передачи кодированной информации
Повышение достоверности передачи в локальных сетях. В локальных сетях дальность передачи информации сравнительно невелика (в пределах одного или нескольких зданий, расположенных на одной территории). При этом организуют последовательный обмен информацией между ЭВМ и периферийными устройствами, образующими локальную сеть. Для передачи по линии связи исходный безызбыточный код (рис. 6.1, а) преобразуется в серии электрических импульсов. С целью повышения достоверности передачи вносят избыточность с помощью изменения формы сигнала или скорости его передачи.
В качестве примера рассмотрим некоторые виды сигнальных кодов (иногда называемых в литературе «линейными», т. е. предназначенными для передачи по линии). Исходный код, обычно называемый NRZ (non return to zero), применяемый в униполярной форме (в виде импульсов тока одного знака), является непомехозащищенным. Лучшими свойствами (при той же энергии сигнала) обладает биполярный код NRZ, где символ 1 передается импульсом положительной, а символ 0 импульсом отрицательной полярности (рис. 6.1, б). Избыточность достигается за счет наличия двух уровней сигнала различной полярности (+ U и – U). Код «Манчестер 11» (рис. 6,1, в) является биполярной сигнальной формой упоминавшегося ранее кода, в котором символ 1 преобразуется в комбинацию 10, а символ 0 — в комбинацию 01. При этом, как и в биполярном коде NRZ, символ передается импульсом положительной, а символ 0 — импульсом отрицательной полярности. Здесь вносится дополнительная избыточность за счет уменьшения скорости передачи информации. Ошибка может быть обнаружена при посимвольном приеме. Ее критерием является заданное превышение продолжительности действия какого-либо из уровней сигнала над временем передачи одного сигнального бита. Положительным свойством кода является несложность обеспечения ввода в синхронизм системы передачи.
В сигнальном коде AMI (alternate mark inversion) (рис. 6.1, г) избыточность вносится с помощью использования (в простейшем случае) трех
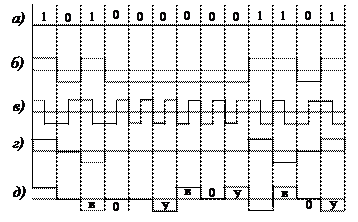 |
 | |||
Рис. 6.1. Примеры кодов последовательного интерфейса ЭВМ
у
уровней сигнала. При этом символы 0 кодируются отсутствием тока, а символы 1 — его наличием с попеременной инверсией полярности. Ошибка обнаруживается при пропуске инверсного импульса.
При использовании простейшего кода AMI возникает сложность в обеспечении ввода системы передачи в синхронизм при передаче длинных последовательностей нулевых символов. В связи с этим более широко распространены его формы, называемые BNZS, где цепочки из N нулей заменяют подстановками знакопеременных символов. Так, в коде BNZS цепочки из трех последовательных нулей заменяют подстановкой BOV или OOV (рис. 6.1, д), где В, V соответственно импульсы, кодируемые по правилам кода AMI и с нарушением этих правил. При выборе вида подстановки необходимо, чтобы число импульсов В между двумя последовательно расположенными импульсами V было нечетным и чередовалась полярность импульсов V. Существуют и другие формы сигнальных кодов.
Внесение асимметрии в канал передачи и применение пошаговой синхронизации. Повышение помехозащищенности при передаче кодовых комбинаций по линии связи может быть достигнуто применением пошаговой синхронизации и широтно-импульсной модуляции с контролем длительности импульсов. Пошаговая синхронизация позволяет обеспечить четкость синхронной работы передающего и приемного устройства и числовой защиты. Различие в длительности передачи символов 1 и 0 позволяет свести к нулю трансформацию вида 1 → 0 и обеспечить d min = 2 даже при передаче исходного безызбыточного кода. Наличие числовой защиты контроля длительности импульсов и пошаговой синхронизации существенно сокращает возможность приема ложных комбинаций при групповых ошибках.
Использование обратного канала. Различают системы с решающей и информационной обратной связью. В системах с решающей обратной связью приемное устройство по избыточности, заложенной в кодовую комбинацию, определяет, относится она к разрешенным или нет. Если да, то приемник исполняет команду и по каналу обратной связи передает уведомление об исполнении. Запрещенную комбинацию приемник не исполняет, а по обратному каналу посылает сигнал переспроса, по которому передается повторное сообщение.
В системах с информационной обратной связью приемник, приняв сообщение, передает его же по обратному каналу. Передающее устройство сравнивает переданное им сообщение с информацией, полученной по каналу обратной связи. При совпадении результатов сравнения передается сигнал, разрешающий исполнение; при несовпадении — сигнал запрета. При необходимости передача повторяется заданное число раз. В простых системах телеуправления при этом обычно используют двоичные неизбыточные коды. В сложных системах с большим объемом передаваемой информации применяют побайтную передачу с контролем по паритету каждого байта и с числовой защитой в конце серии. Это позволяет обнаруживать ошибки в приеме того или иного байта, не дожидаясь окончания передачи всего сообщения.
Мажоритарное декодирование. При этом методе в канал связи передается не менее трех одинаковых кодовых комбинаций. Решение о правильности принимается по большинству одинаковых принятых комбинаций. Например, если переданы три комбинации и на приемной стороне две из них совпали, то разрешается исполнение команды («метод голосования»).
Поиск по сайту: