Системи числення, які використовуються в комп'ютерах

Система числення з основою N=2 є позиційною системою числення і нічим не відрізняється від позиційної система числення з будь-якою основою.. Але для комп'ютера ця система числення має вагомі переваги, які полягають у тому, що її алфавіт має всього два символи. Для фіксації цих символів достатньо мати деякий пристрій, що може мати два суттєво різних і стійких стани.

Для людини двійкова система є громіздкою. їй звична десяткова система, у якій відпрацьовані прийоми записування чисел по його імені, визначення імені по запису, визначення ваги числа по його запису й імені, відпрацьовані прийоми додавання, віднімання, множення й ділення будь-яких чисел. У двійковому записі числа важко визначити його значення, немає поняття імені саме двійкового числа, важко зіставити ланцюжок 1 і 0 із його змістом. Виникає потреба перетворювати двійкові записи у десяткові і навпаки.

Приклади:

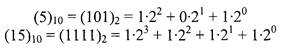
В обчислювальній техніці і програмуванні значне місце займають вісімкова й шістнадцяткова системи числення. Вони використовуються для скороченого запису двійкових кодів.

У вісімковій системі числення в якості цифр використовують символи: 0, 1,2, 3, 4, 5, 6, 7. В шістнадцятковій системі потрібно 16 символів, в якості яких використовують арабські цифри і п'ять букв латинського алфавіту, що утворюють послідовність (із врахуванням ваги шістнадцяткових цифр): 0, 1,2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F.

Приклади:

Десяткові еквіваленти символів А, В, С, D, E, F:

Переведення чисел із десяткової системи числення у будь-яку іншу

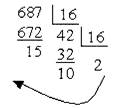
Переведення цілого числа з десяткової системи числення у будь-яку іншу здійснюється шляхом послідовного ділення числа на основу нової системи числення. Ділення виконується до тих пір, поки остання частка не стане менше дільника. Отримані остачі від ділення, взяті у зворотному порядку, будуть значеннями розрядів числа в новій системі числення. Остання частка дає старшу цифру числа.

Приклад:

Приклад:

Приклад: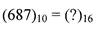

Для переведення правильного дробу з десяткової системи числення у будь-яку іншу потрібно помножити заданий дріб на основу нової системи числення. Отримана ціла частина добутку буде першою цифрою після коми дробу в новій системі числення. Далі по черзі множаться дробові частини добутків на основу нової системи. Отримані цілі частини добутків будуть цифрами дробу у новій системі числення. Цей процес продовжують до тих пір, поки не буде знайдено число із заданою точністю.

Приклад:

Приклад:

Для переведення змішаного числа з десяткової системи числення в іншу необхідну окремо перевести цілу й дробову частини за вказаними правилами, а потім об'єднати результати у змішане число.

Переведення чисел із будь-якої системи числення в десяткову

Для переведення чисел із будь-якої системи числення в десяткову необхідно це число представити у вигляді полінома і розкрити всі члени полінома в десятковій системі числення.

Приклад:

Приклад:

Переведення з т-ї системи числення в десяткову виконуєть­ся шляхом додавання добутків усіх відповідних десяткових еквівалентів символів числа в т-й системі на вагу відповідного знакомісця.

Приклад переведення з шістнадцяткової системи числення в десяткову систему:

Поиск по сайту: