АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Существует другой способ

Читайте также:
  1. B. Способом “рот-в-рот”.
  2. E. Загасити палаючий одяг будь-яким способом, терміново евакуювати в лікувальну установу
  3. Exercises for Lesson 3. Requests and offers / Просьбы и предложения. Способы выражения, лексика, примеры.
  4. Exercises for Lesson 3. Requests and offers / Просьбы и предложения. Способы выражения, лексика, примеры.
  5. Exercises for Lesson 3. Requests and offers / Просьбы и предложения. Способы выражения, лексика, примеры.
  6. I. Первым (и главным) принципом оказания первой помощи при ранениях нижней конечности является остановка кровотечения любым доступным на данный момент способом.
  7. II. Способы изменения обязательств (цессия, суброгация, делегация)
  8. II. Способы приобретения права собственности на движимые вещи
  9. II. Способы решения детьми игровых задач
  10. II. Способы решения детьми игровых задач
  11. III. Способы прекращения обязательств
  12. IV. Правоспособность физического лица и ее ограничения

Выполнение условия сходимости можно добиться с помощью перехода от исходного уравнения к эквивалентному виду следующим образом: умножим обе части первого уравнения на неравную нулю константу и прибавим к обоим частям уравнения х, получим . Обозначим , тогда . Константа выбирается так, чтобы выполнялось достаточное условие сходимости итерационного, т.е. .

Это условие равносильно неравенствам ,

Откуда при

и при .

Требуемую точность вычислений можно обеспечить использованием оценок приближения к корню :

1) ;2) .

При второе неравенство примет вид . Таким образом, если , то . Очевидно, что чем меньше , тем быстрее сходится процесс итераций.

 

Процесс итераций заканчивается при выполнении двух критериев!!!!!

1) два последних приближения отличаются между собой по модулю на заданную величину : .

(Этого критерия недостаточно, так как в случае крутизны графика, указанное условие будет выполнено, но может находиться далеко от корня);

2) мера удовлетворения уравнению последнего приближения корня: .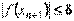

(Отдельно второго критерия недостаточно, так как при пологом графике функции условие может быть выполнено, но может быть далеко от корня.)

 

 

F Пример 1.

Имеем уравнение 2х + lg(2x + 3) = 1. Необходимо уточнить корень с погрешностью  < 0,001.

@ Решение

Запишем f(х) = 2х + lg(2x +3) – 1. Проведя процедуру отделения корней, получим, что корень находится в промежутке [0;0,5], т. е. а = 0, b =0,5.

Приведем уравнение f(х)=0 к виду, удобному для итераций: (х) = х. Для этого уравнение 2х + lg(2x +3) –1=0 выразим следующим образом:

f(х) = х= 0,5 – 0,5 lg(2x +3).

Найдем первую производную функции f'(x):

f'(x)= -0,5·lg(е)/(2х+3)·2 = – lg(е)/(2х+3); lg(е)» 0,4343;

f'(0)= -lg(е)/(2·0+3) = – 0,1448; f'(0,5)= -lg(е)/(2·0,5+3)= – 0,1086.

Следовательно, на отрезке [ 0;0,5 ] |f'(х)| £ 1 и к уравнению можно применить метод итерации.

За начальное приближение возьмем х0 =0, все остальные прибли­же­ния будем определять из равенства: хi+1 = 0,5 – 0,5 lg(2xi +3),результаты сведем в табл. 3.8.

Таблица 3.8


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)