Колебания и волны

Литература

1. Ремизов А.Н. «Медицинская и биологическая физика»,М.2001 г.

2. Блохина М.Е., Эссаулова И.А. и др. «Руководство к лабораторным работам по медицинской и биологической физике»

3. Кумыков. В.К., Захохов Г.М. «Физические методы в функциональной диагностике» Нальчик, КБГУ,2006

4. Кумыков. В.К., Абазова З.Х «Физические методы в медицинских технологиях» Нальчик, КБГУ, 2004

Лекция №1

Колебания и волны

1. Гармонический осциллятор. Колебательные системы в биологии и медицине.
2. Механические волны, их уравнение. Вектор Умова. Ультразвук, его применение в медицине.
3. Эффект Доплера, его медицинские приложения

1. Колебания гармонического осциллятора являются очень важным примером периодического движения. К числу классических систем, аналогичных гармоническому осциллятору, относятся любые системы, которые, будучи слегка выведены из положения равновесия, совершают устойчивые колебания. К ним относятся:

1. Математический маятник в пределах малых углов отклонения.
2. Масса на пружине в пределах малых амплитуд колебаний
3. Колебательный контур, состоящий из конденсатора и катушки

Частота колебаний осциллятора не зависит от амплитуды.

Математический маятник состоит из материальной (∙) массой m, расположенной на нижнем конце невесомого стержня длиной L, свободно вращающегося вокруг оси, проходящей через верхний конец.

Выведем уравнение колебаний маятника. Проще всего записать уравнение F=ma, однако поучительнее будет решить поставленную задачу через закон сохранения энергии. Отклонение маятника определяется углом , который стержень образует с вертикалью.

(1)

Потенциальная энергия маятника

U()=Mgh (2)

(3)

Кинетическая энергия маятника равна

(4)

Полная энергия маятника равна

(5)

Принимая во внимание, что 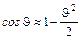(6)

(7)

Решая это уравнение относительно находим

(8)

При . Тогда из (7) получим с учетом того, что :

, (9)

Тогда (8) перепишется в виде:

(10)

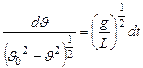Или (11)

Этот вид удобен для интегрирования. Если начальные условия таковы, что при , то

(12)

(13)

Так как , то (13) запишется

(14)

Или (15)

Где 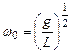- круговая частота

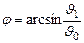-фаза

Период колебаний математического маятника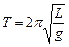

пружинного

колебательного контура

Поиск по сайту: