 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вероятность безотказной работы. Так как безотказная работа и отказ – взаимно противоположные состояния изделия, их сумма равна единице:
| (2) |
Так как безотказная работа и отказ – взаимно противоположные состояния изделия, их сумма равна единице:
 .
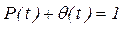| (3) |
При анализе зависимостей (1) и (2) следует, что при t=0, Nот=1, 
, следовательно, 
; при t ®¥ Nот= N0, 
, Р(t) =0.
Следовательно, вероятность безотказной работы за рассматриваемый промежуток времени изменяется в указанных пределах. Покажем, что кривой, соответствующей этому изменению, является экспонента.
3. Плотность вероятности отказов f(t), или вероятность отказов в единицу времени, есть производная от функции вероятности отказов по времени или наработке в других единицах:
 ,
| (4) | |
 .
| (5) |
Выразим вероятность отказов и вероятность безотказной работы через плотность вероятности отказов. По определению
|
вероятность отказов за определенный промежуток времени равна сумме плотностей вероятностей отказов в промежутке времени и при t®¥:
|  ,
|
что следует из предыдущих рассуждений. Из выражения (3)
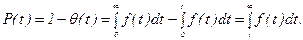
| (6) |
4. Интенсивность отказов l(t)– это вероятность отказа в единицу времени при условии, что отказ до этого времени не наступал, то есть это скорость изменения отказа в единицу времени, отнесенная к числу исправных элементов (постоянных в указанном промежутке времени):
 .
| (7) |
Из выражений (4) и (7) следует, что f(t) и l(t) отличаются знаменателями. Первое определяется относительно N0, а второе – N и.
Из выражений (4) и (5) следует
|
Умножив числитель и знаменатель на N и, получим
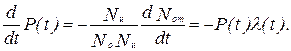
| (8) |
Преобразуя выражение (8), получим:
 .
|
Проинтегрируем:
 ,
|
получим
 ,
|
или
 .
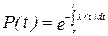| (9) |
При нормальной эксплуатации объектов интенсивность отказов l(t)=const.= l, тогда
принимает выражение lt, а зависимость (9) представляется как
 .
| (10) |
Из этого следует, что вероятность безотказной работы изменяется по экспоненте (рис. 1).
Рис. 1. Характер изменения безотказной работы Р(t) объекта
в зависимости от пробега (l)
В математической статистике закон распределения случайной величины Х может быть задан в аналитическом виде или таблицей, где против каждого возможного Х=хi стоит соответствующая вероятность pi.
. (12)
Pc(t)=[1-θ1(t)][1-θ2(t)]…[1 θn(t)]≈1[θ1(t)+θ2(t)+…θn(t)]
(t)=θ3(t)=…θn(t),θc(t)=θ1n(t)
и тогда
.
K = R\ Δx
х.
P(t)=θ′(t)
, т.е. при длительной эксплуатации ремонтируемого изделия поток отказов становится стационарным. Наработка на отказ Т0 является наглядной характеристикой надежности, поэтому широко используется на практике.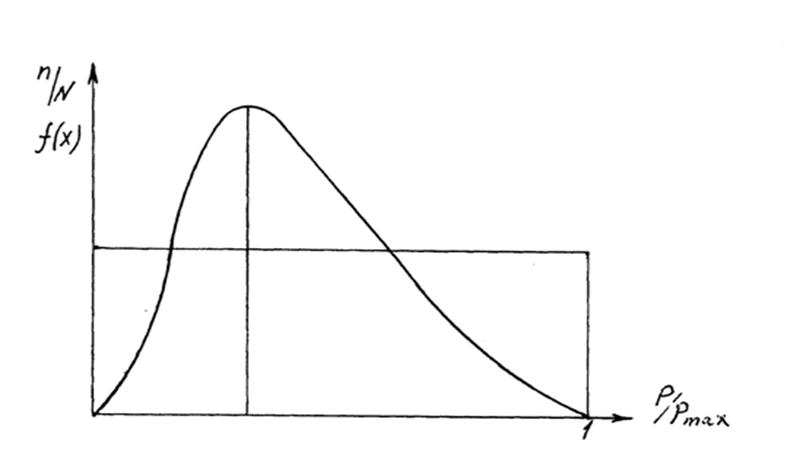
Рис. 6. Кривая относительного изменения нагрузки
Для вновь создаваемых машин эту функцию можно рассматривать как плотность вероятности (плотность распределения) f(x);
· затем строят функцию распределения F(x) (рис. 7), причем функции F(x) и f(x) связаны известным соотношением f(x)=F’(x). Функция f(x) показывает вероятность работы с каждым значением нагрузки, а площадь, очерчиваемая кривой функции распределения, равна единице.
Рис. 7. Функция распределения
Распределение нагрузок для разных машин сводят к четырем известным типовым, хорошо изученным в математике кривым (рис. 8), которые определяют следующие режимы работы: СР – средний равновероятностный, T (или b-распределение – тяжелый), С(н) – средний нормальный (Гауссово распределение), Л (или g-распределение) – легкий.
Функция вероятности распределения нагрузок для каждого из них известна. Так, для кривой С(н) она равна:
F(x) = (1/s√2π)•∫℮-(x-x¯)2/2S2dx, 
где x = 0,5 Xmax, s = 0,2 Xmax.
Многочисленные исследования нагрузок, возникающих при эксплуатации машин, позволяют сделать следующий вывод: режим работы С(н) характерен для большинства универсального оборудования; режим СР – для более интенсивно эксплуатируемого специализированного оборудования; режим Т – для горного оборудования.
Рис. 8. Типовые (расчетные) режимы работы машин
Динамические нагрузки всегда возникают при работе машины. Большинство машин работает в условиях прерывистого рабочего процесса, и динамические нагрузки неизбежно связаны с разгоном, торможением и реверсированием. Все механизмы возвратно-поступательного и периодического движения (кривошипно-ползунные, кулисные) работают в динамическом режиме нагрузок. Большинство динамических нагрузок возникает из-за недостаточной уравновешенности быстровращающихся деталей. Так, смещение на 0,1 мм центра тяжести от оси вращения ротора, вращающегося со скоростью n=3000 об/мин, приводит к возникновению центробежной вращающейся силы, равной силе тяжести ротора, действие которой многократно опаснее действия самой силы тяжести. При вращении вала на подшипниках скольжения возникает нестабильная работа (вал “плавает”, возможны вибрации), а при установке валов на подшипниках качения без натяга возникает проскальзывание тел качения, повышается износ. Некоторые машины, работающие в зарезонансной области, при разгоне и остановке проходят резонансные зоны. При зависимости момента на валу привода от частоты вращения может возникнуть возрастание моментов при прохождении через зоны резонансов, что необходимо учитывать при расчете деталей на усталость. В прямозубых передачах вход в зацепление вызывает ударные нагрузки, определяемые упругостью зуба (упругая деформация и погрешность основного шага). Кроме того, знакопеременность силы трения при прохождении зуба через полюс зацепления вызывает динамические нагрузки. Динамическая неустойчивость ременных передач объясняется биением шкивов, неоднородностью ремня, крутильными колебаниями шкивов при малых скоростях ремней. В валах с подшипниками качения переменная жесткость подшипников по углу поворота может вызвать вибрации. При расчетах колебаний приводов машин необходимо учитывать упругость и демпфирование электромагнитной связи между статором и ротором приводного двигателя, так как электродвигатели представляют собой мощные демпферы.
Рис. 9. Схема механизма сцепления автомобиля
При переключении скорости выжимается сцепление и рычаги 10 через подшипник 7, систему рычагов 6 отводят нажимной диск 3 и диски сцепления 2, отключая движение от двигателя. Передача переключается. Затем плавно отпускается педаль сцепления, рычаги 10 и 6 под действием пружин 4 плавно возвращают нажимной диск сцепления в исходное положение, обеспечивая движение от маховика 1 на вал 9 коробки скоростей и дальше на ведущий мост автомобиля. При этом плавность движения автомобиля определяется плавностью прижатия фрикционных дисков 2.
Рис. 10. Фланкирование зубьев колес
Увеличение тел качения в подшипниках достигается заменой шариковых подшипников на роликовые, а последних – на игольчатые.
На рис. 11 приведена схема резания при токарной обработке наружной цилиндрической поверхности. Толщина стружки t в основном определяет величину силы P и ее ориентацию относительно оси Z. Если создать в шпиндельной опоре (передней) систему с явно выраженными неравными жесткостями, то, ориентируя силу Р под углом a относительно оси максимальной жесткости C1 системы, можно добиться безвибрационного резания, что снижает динамическое нагружение на опору и повышает качество обработки поверхности. Оптимальное значение угла a лежит в пределах 5-8 градусов.
Рис. 11. Упругая система с ориентированными осями жесткости при резании
Схема стиральной машины типа СМА-4 показана на рис. 12. Стиральный барабан 2 имеет горизонтальную ось вращения, поэтому, особенно при отжиме белья, возникают значительные динамические нагрузки, которые воспринимаются и снижаются пружинами 4 и амортизаторами 3.
Рис. 12. Схема стиральной машины-автомата типа СМА-4
В стиральных машинах-полуавтоматах (рис. 13) снижение динамических нагрузок обеспечивается следующими конструктивными изменениями. Активатор 2 имеет вертикальную ось вращения и расположен на дне стирального бака, а отжимной барабан 3 имеет вертикальную ось вращения, что обеспечивает качественный отжим белья при сушке.
Рис. 13. Схема стиральной машины-полуавтомата
Рис. 14. Двухмассовая крутильная система
Пусть на маховик с моментом инерции 
действует переменный момент М0 sinwt. Если вал рассматриваем как жесткий, то этот момент разделится между узлами системы пропорционально их моментам инерции Q1 и Q2. Тогда амплитуда переменного момента, который передается машине, M1 равна:
Рис. 19. Деформация витков резьбы и распределение нагрузки по виткам
Задача о распределении нагрузки по виткам была впервые решена Н. Е. Жуковским, который показал, что при взаимодействии крепежного винта с гайкой, имеющей 10 витков, первый, наиболее нагруженный виток воспринимает 34 % нагрузки, а десятый, наименее нагруженный, – менее 1 %.
Уменьшения концентрации нагрузки можно добиться некоторыми конструкторскими решениями:
· выполнением гайки, резьбовая часть которой полностью или частично размещается в отверстии под опорной поверхностью (рис. 20, а) или изготовлением гайки с кольцевой выточкой (рис. 20, б). Такая выточка повышает предел выносливости болта в 1,6 раза;
· изготовлением угла профиля крепежной резьбы винта на 5 градусов больше угла профиля гайки (650 и 600 для метрической и дюймовой резьбы соответственно) (рис. 20, в). В этом случае витки гайки будут работать вершинами, что увеличивает длину консоли и увеличивает податливость витков и приводит к выравниванию нагрузки по длине гайки;
Рис. 20. Уменьшение концентрации напряжений в резьбах
· выполнением отверстия в гайке слегка коническим, что обеспечивает переменную податливость витков (рис. 21, а). Витки нагружают не по всей высоте, нагрузки смещаются от заделки, и податливость увеличивается – предел выносливости винта повышается примерно на 20 %;
· выполнением конической проточки с поднутрением около 5 градусов (рис. 21, б). Проточка охватывает только наиболее нагруженные витки, что приводит к их разгружению, и ресурс винта может увеличиться на 85 %.
Рис. 21. Изменение конструкции гайки для снижения концентрации нагрузки
Концентрация нагрузки при сжатии. Резкая концентрация нагрузки возникает при сжатии двух тел по площади, если поверхность одного из них выходит за контур контакта (рис. 22).
Рис. 22. Концентрация нагрузки у кромок при сжатии двух тел по площади
Концентрацию давления у кромок можно представить следующим образом. Рассмотрим под поверхностью контакта элементарные параллелепипеды (рис.22). На каждый из них и на соседние передается внешнее давление, которое заставляет их деформироваться и проседать; только крайние находятся в особых условиях, так как их соседние элементы с одной стороны не нагружены, поддерживают их и придают им дополнительную жесткость. От этого возникает пика давлений, которая теоретически уходит в бесконечность.
Соединения с гарантированным натягом являются наиболее характерным примером возникновения пиков давлений у кромок (рис. 23, а).
В результате концентрации давления и фретинг-коррозии усталостная прочность валов резко снижается. Понижение прочности вала от напрессовки может быть полностью компенсировано комплексом следующих мероприятий: увеличением диаметра посадочной поверхности 1 вала точно по длине ступицы на 5 %, выполнением галтелей 2 большего радиуса R и их обкаткой, выполнением на ступице разгрузочных канавок 3 (рис. 23, б).
Рис. 23. Регулирование концентраций напряжений в соединении с натягом
Концентрация нагрузки от сжатия характерна и для подшипников качения. Если рассматривать подшипник качения, нагруженный радиальной силой, то можно отметить, что под действием нагрузки кольца смещаются, причем тела качения деформируются и нагружаются неодинаково (рис. 24).
Рис. 24. Изменение нагрузки по телам качения опорных подшипников
В этой постановке сближение рассматривается как сжатие тел качения, а кольца условно считаются жесткими. Сжатие тел качения в плоскости нагружения максимально и равно смещению колец d (d=y1). В беззазорном подшипнике сжатие шарика или ролика под углом Q равно y2 = d ·cosQ. Исходя из этого условия уравнения равновесия и зависимости между нагрузкой на тело качения и сближением колец определяют нагрузку на тело качения:
· для шарикоподшипников (беззазорных) нагрузка на наиболее нагруженный шарик Р0=4,37 R/z, где R – радиальная нагрузка на подшипник, z – число тел качения (в реальном подшипнике Р0@ 5 R/z);
· для роликоподшипников Р0=4 R/z (в реальном роликоподшипнике Р0@ 4,6 R/z).
Распределение нагрузки (рис. 25) может быть несколько улучшено эллиптической расточкой отверстия под подшипник с расположением большей оси вдоль нагрузки (у В.А. Кудинова сила резания ориентируется под углом b к оси максимальной жесткости для снижения автоколебаний при точении). О более благоприятном распределении нагрузки на шпиндельной опоре судят по изменению величины “предельной” толщины стружки при точении.
Рис. 25. Выполнение ориентированных осей жесткости в опорах с подшипниками качения
Эффективного снижения уровня автоколебаний при растачивании добиваются созданием ортогональных осей жесткости в передней шпиндельной опоре расточного станка. Для этого овальным (в пределах допуска) выполняют посадочное место внутреннего кольца подшипника.
Рис. 26. Зависимость предельной стружки от ориентации оси максимальной жесткости С1
На рис. 26 показано изменение величины “предельной” стружки tпр при различной ориентации оси максимальной жесткости C1 относительно силы резания Pz. При обычном исполнении шпиндельного узла tпр изменяется от 2 мм до 2,3 мм. У шпиндельного узла с ориентированными осями жесткости tпр достигает 8 мм. Точность обработанных поверхностей на латунных образцах не изменяется в сравнении с обычными опорами, а чистота имеет тенденцию к улучшению.
Однако этот способ сложен технологически: трудно выполнить эллиптическое посадочное место. В целях изыскания дополнительных средств повышения виброустойчивости (надежности) при растачивании были спроектированы составные борштанги (рис. 27).
Рис. 27. Виброустойчивая борштанга
К корпусу 1, укрепляемому в шпинделе расточного станка, крепится резцедержка 3, соединяемая с корпусом посредством резьбы и проставочного кольца 5 между резцедержкой и корпусом. На проставочном кольце выполняются симметричные относительно его оси скосы Б и В, обеспечивающие создание явно выраженных осей максимальной и минимальной жесткостей, собранной оправки. Максимальная виброустойчивость обеспечивается при примерном совпадении оси максимальной жесткости с направлением действия силы резания (tпр увеличивается в 1,7 раза); оптимальным является отношение жесткостей 1,22.
Применение составных оправок увеличивает технологические возможности при растачивании. Например, при использовании составной оправки с l/d = 5 величина предельной стружки увеличивается в 4 раза по сравнению с обычной оправкой. Точность и чистота обработанной поверхности сохраняются по сравнению с цельной оправкой, наблюдается тенденция к улучшению чистоты обработанной поверхности.
Концентрация нагрузки, вызываемаяизгибом. Такой вид нагружения характерен для валов на опорах качения и скольжения и зубчатых передач. Для вала на опорах скольжения (рис. 28, а) эпюра давления становится резко несимметричной и сильно снижает запас надежности. Для таких опор характерно снижение давления до “0” на свободных концах подшипника. Ближний к силе конец опоры воспринимает максимум нагрузки.
Рис. 28. Концентрация нагрузки в подшипниках скольжения жидкостного трения
В опорах полужидкостного трения (рис. 29) давление резко возрастает на кромках.
Рис. 29. Концентрация нагрузки в подшипниках полужидкостного трения
Исследование характера распределения нагрузки в подшипниках и разработка рекомендаций уменьшения концентрации нагрузки являются сложной инженерной задачей. В этом направлении ведется работа в ведущих исследовательских машиностроительных институтах мира. Разработан ряд рекомендаций:
· применяют узкие подшипники с малым отношением l/d,
где: l – длина, d – диаметр подшипника. Они повышают жесткость валов, используют самоустанавливающиеся подшипники. В подшипниках скольжения, изготавливаемых в габаритах подшипников качения, l/d = 0,3…0,4, в подшипниках быстроходных поршневых двигателей внутреннего сгорания l/d – 0,5…0,6, в подшипниках дизелей l/d – 0,6…0,9;
· применяют самоустанавливающиеся сферические опоры, конструктивная схема которых показаны на рис. 30,а. Наиболее совершенно использование сегментных подшипников с самоустановкой в двух плоскостях. В качестве шарниров сегментных подушек подшипников применяют: шаровые фрикционные шарниры (рис. 30,б), упругие шарниры (рис. 31,а) и шарниры качения (рис. 31,б);
· подшипники скольжения особо ответственных валов (шпиндели металлорежущих станков) пришабривают по валу в нагруженном состоянии.
Рис. 30. Самоустанавливающиеся подшипники
Рис. 31. Самоустанавливающиеся сегментные подшипники
Деформация вала вызывает неравномерное распределение нагрузки по длине ролика в роликоподшипниках, причем ролики часто работают не по всей длине. Снижение нагрузок в роликоподшипниках обеспечивают изготовлением рабочей поверхности наружного кольца в виде гиперболоида вращения (рис. 32,а). Технологически это легко обеспечить, наклонив ось шлифовального круга. Иногда для снижения кромочных давлений по концам роликов их выполняют бомбинированными со стрелой выпуклости 0,01-0,02 мм (рис. 32,б.) Это повышает ресурс подшипников по данным ВНИ подшипниковой промышленности в 2-3 раза.
Рис. 32. Изменение конструкции роликоподшипников
Конструкции с двумя подшипниками качения в опоре валов приводят из-за деформации валов к резко неравномерному распределению нагрузки между подшипниками. Для повышения несущей способности опоры применяют радиально-упорные подшипники в компоновке, имитирующей двухрядный самоустанавливающийся подшипник (рис. 33, а). Иногда подшипники в опоре ставят вершинами конусов контакта в разные стороны (рис. 33, б). При этом опоры как бы раздвигаются, вал приобретает повышенную жесткость за счет дополнительной нагрузки опор.
Рис. 33. Схемы установки сдвоенных подшипников в опоре
Приведенные примеры позволяют при конструировании принимать инженерные решения, снижающие концентрацию нагрузки, что приводит к повышению надежности.