 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Язык описания сборочных единиц
Геометрическая информация о сборочной единице (изделии) содержится в сборочном чертеже. Одной и той же сборочной единице (СЕ) может соответствовать неограниченное множество моделей М.
Рассматриваемая геометрическая модель СЕ предназначена для решения следующих задач проектирования ТП:
- моделирование силового замыкания с целью выявления сборочных размерных
цепей (СРЦ) и назначение допуска на составляющие звенья (детали);
- выявление геометрических свойств СЕ и элементов, позволяющие распоз-
навать условия базирования деталей;
- выявление возможности установления промежуточных СЕ и последова-
тельности сборки;
- выявление свойств элементов СЕ с целью определения условия базирования;
- определение характеристик точности относительного расположения поверхно-
стей замыкающего звена.
Исходя из служебного назначения СЕ и составляющих элементов следует, что передача силовых потоков осуществляется с помощью контактов базовых поверхностей, т.е. вспомогательных поверхностей базовой детали и основных баз присоединяемой детали, поэтому геометрическая модель СЕ имеет двухуровневую иерархическую структуру:
где 
базовое множество, состоящее из деталей СЕ;
множество отношений на 
;
,
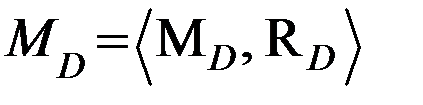где 
базовое множество поверхностей, ограничивающих деталь D;
множество отношений на М D.
Таким образом, элементы базового множества МСЕ модели МСЕ, в свою очередь, представляют модель МD, которая содержит в качестве базового множества элементы нижнего уровня – ограничивающие поверхности. Отсюда иерархическая структура модели МСЕ определяется следующими уровнями элементов базового множества: сборочная единица – деталь – поверхность.
Рассмотрим множество отношений RCE, которые разбиваются на следующие группы:
1) Унарные отношения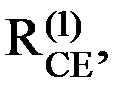 
которые характеризуют свойства элементов СЕ – деталей.
2) Бинарные отношения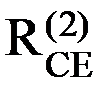 
на множестве МСЕ, которые характеризуют взаимосвязи между деталями сборочной единицы.
3) Унарные отношения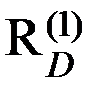 
элементов базового множества М D.
4) Бинарные отношения 
на множестве всех поверхностей деталей.
5) п- арные отношения, которые определяют свойства подмножеств множества М быть сборочной единицей; эти отношения задаются в неявном виде с использованием правил вывода.
Отношения первой группы
Унарные отношения 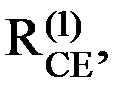определяющие следующие свойства деталей, принадлежащих СЕ:
- характеристики, указанные в спецификациях сборочного чертежа (шифр детали, наименование, марка конструкционного материала, масса, габаритные размеры);
- параметры расположения делали в системе координат, связанной с СЕ (параллельный перенос собственной системы вдоль координатных осей и вращение вокруг этих осей).
Унарные отношения, определяющие параметры расположения детали, могут задаваться как в явном виде путем непосредственного считывания размеров деталей с чертежа, так и в неявном – путем указания поверхностей контакта со смежными деталями.
Отношения второй группы
Это бинарные отношения 
на множестве деталей, принадлежащих СЕ, устанавливают для каждой пары деталей Di и Dj факт их взаимодействия при функционировании сборочной единицы.
Будем говорить, что детали Di и Dj находятся в отношении 
если они взаимодействуют друг с другом в СЕ.
Моделью отношения может служить граф взаимосвязей G «деталь – деталь», который определяется так
где Р – множество вершин (входящие детали и сборочные единицы нижнего уровня);
U – множество дуг, соединяющие пары вершин.
На рисунке 8.3 показан кондуктор для сверления радиальных отверстий, а соответствующий ему граф G взаимодействия «деталь-поверхность) на рисунке 8.4, на рисунке 8.5 показан граф связей «деталь-деталь».
Рисунок 8.3
Рисунок 8.4
Рисунок 8.5
Рассмотренное бинарное отношение широко используется при разработке алгоритмов выявления сборочных размерных цепей.
Отношения третьей группы
Унарные отношения 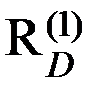на множестве МD поверхностей детали. Эти отношения определяют свойства поверхностей детали, которые не отражены в модели М, то есть свойства поверхностей быть основной или вспомогательной базой. Эти свойства поверхностей можно выявить лишь с позиции СЕ, включающей рассматриваемую деталь.
Говорят, что поверхности πi и πj деталей Dk и Dl находятся в отношении
R(2)(Dk, Dl), если они взаимодействуют между собой в сборочной единице.
Для кондуктора, изображенного на рисунке 8.3 свойства R(1) (тип базы) поверхностей деталей отражены в таблице 8.2.
Таблица 8.2
Унарные отношения третьей группы можно дальше детализировать до количества степеней свободы с учетом ориентации детали. К этим отношениям относятся также тип и точность посадки сопряжения рассматриваемой детали со смежными деталями.
Отношения четвертой группы
Это бинарные отношения на множестве всех поверхностей и деталей, принадлежащих СЕ.
Отношение может быть представлено в виде графа
где Р – множество вершин (
), где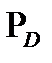 
- множество деталей; 
- множество поверхностей; 
- множество дуг; uij = (pi, pj), если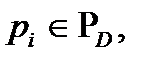 
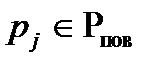. причем дуга 
имеет ориентацию от 
к 
.
Отношения пятой группы
п- арные отношения, позволяющие определить, является ли произвольное подмножество множества М деталей сборочной единицей или нет. Эти отношения невозможно определить в явном виде, но можно установить лишь алгоритмически с использованием правил вывода. К важнейшим свойствам относятся свойства базирования и доступности.
Поиск по сайту: