 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Геометрическими моделями деталей
Лекция 8 ММ ТП в маш
Установление изоморфных отображений между
геометрическими моделями деталей
Одна и та же деталь может иметь неограниченное множество геометрических моделей, каждая из которых предпочтительна при решении задач отображения и проектирования ТП при проектировании сквозных САПР (конструкция – технология – изготовление или CAD-CAM-CAE), большое теоретическое и практическое значение имеет установление связей (интерфейсов) между геометрическими моделями. Решение этой проблемы позволяет автоматизировать процесс передачи геометрической информации от одного типа проектирования к другому, а также устанавливать обратные связи от более поздних этапов проектирования к более ранним. Последнее имеет особое значение, так как конструктор-проектировщик имеет возможность отрабатывать конструкции изделия на технологичность на ранних стадиях проектирования. Особое место в множестве геометрических моделей занимают модели логико-алгебраического типа.
Важность логико-алгебраической модели определяется тем, что с ее помощью устанавливаются гомоморфные отображения с проблемными геометрическими моделями (МТП, МТО, МСАП ЧПУ) (рисунок 8.1). В частности, логико-алгебраическая модель М позволяет определить необходимые свойства поверхностей, необходимые для проектирования ТП механической обработки, а так же все геометрические свойства обрабатываемой заготовки, требуемые для расчета управляющих программ ЧПУ, т.е. модель М обладает свойствами универсальности.
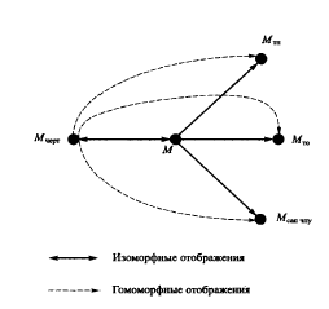
Рисунок 8.1
Попытки устанавливать прямые связи между моделями чертежа и проблемными моделями бесперспективны, потому что указанных связей должно быть столько, сколько разновидностей проблемных моделей. Поэтому с изменением геометрических моделей каждый раз возникает необходимость разработки соответствующих программных интерфейсов.
Из сказанного следует необходимость установления изоморфных связей между геометрическими моделями чертежа и логико-алгебраической модели.
Напомним, что модели М и M’ называются изоморфными, если между ними можно установить такое взаимно-однозначное соответствие, при котором для любых элементов a, b из М и соответствующих им элементов a’ и b’ из M’ сумме a + b соответствует сумма a’ +b’, а произведению ab соответствует произведение a’b’.
Модели M и M’ называются гомоморфными, если между ними можно установить такое отображение φ, при котором всякому элементу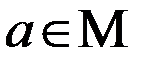 
ставящее в соответствие однозначно определенный элемент 
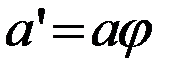, из M’ (
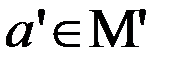) и если для 
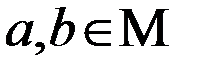имеет место 
.
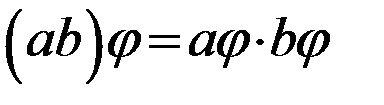Очевидно, что потребовав от гомоморфизма дополнительно взаимную однозначность отображения φ, получим изоморфизм.
Отображение – закон, по которому каждому элементу х некоторого заданного множества Х сопоставляется однозначно определенный элемент у другого заданного множества У (при этом Х может совпадать с У). Такое соотношение между элементами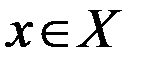 
и 
записывается в виде:
Говорят, что отображение f действует из X в Y и пишут:
или 
.
Если X и Y числовые множества (элементами этих множеств являются некоторые числа), то отображение f называется функцией.
Если множество Х – числовое множество, а множество Y – функциональное множество (множество, элементами которого являются функции), то отображение f называется функционалом.
Если X и Y являются функциональными множествами, то отображение f называется оператором.
Отношение – произвольное подмножество R множества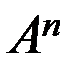 
всех кортежей (упорядоченных наборов) вида 
где 
элементы некоторого множества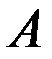 
; в этом случае говорят, что R есть п – местное (п – арное) отображение
При п =0 - нульарное отношение; п = 1 - унарное отношение; п = 2 – бинарное отношение; п = 3 – тернарное отношение и т.д..
Понятие отношения служит в математике для выражения на теоретико-множественном языке связей между объектами. Обобщением понятия «отношение» является соответствие.
Возвращаясь к установлению изоморфных связей между геометрическими моделями чертежа Мчерт и моделями логико-алгебраического типа отметим, что 
где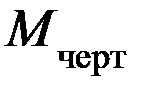 
- базовое множество элементов (отрезки прямых, дуги, окружности, полулинии и другие одномерные многообразия на плоскости); 
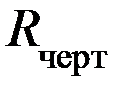- множество отношений. 
Множество 
можно разбить на две группы:
- унарные отношения (свойства) R(1) элементов множества 
;
- парные отношения R(n) (n ≥ 2).
Рассмотрим эти группы отношений на примере фланца (рисунок 8.2)
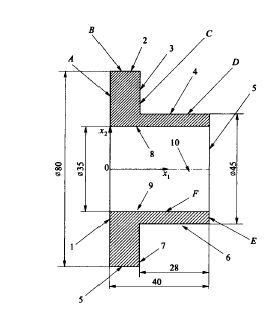
Рисунок 8.2
Первая группа отношений определяет свойства элементов, регламентированных графической системой: типы цветов и линий. К этой группе относятся унарные отношения, определяющие значения координат на плоскости (параметров) на плоскости:
-четыре координаты двух точек отрезка прямой на плоскости или шесть
координат в пространстве;
- координаты центра и радиус окружности;
- координаты трех точек дуги.
Начало координат в абсолютной системе имеет координаты (50, 100). Все отрезки прямых пронумерованы от 1 до 10. Каждый отрезок характеризуется шестью геометрическими параметрами: три координаты начальной точки и три координаты конечной точки отрезка. Например, отрезок LINE9 содержит шесть координат двух точек: первая точка (50, 82.5); вторая точка (90, 82.5); отрезок 10 имеет тип CENTER, а отрезки LINE1 … LEINE9 имеют тип CONTINUOS.
Вторая группа отношений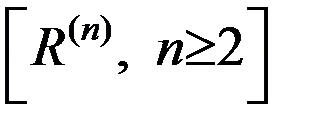 
получается на основе использования элементов модели 
и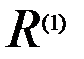 
, а также правил преобразования отношений с использованием формул аналитической геометрии. Множество отношений второй группы потенциально неограничено, поэтому необходимо выделить из них те, которые связаны с образованием модели М.
Примером выделенных отношений R могут служить
- перпендикулярность БЭФов, параллельность, соосность и др.;
- принадлежность элементов поверхности.
Поверхности, ограничивающие деталь, показаны буквами латинского алфавита ABCDF. При построении логико-алгебраической модели М на основе модели М черт необходимо установить связь (интерфейс) между множеством чертежных примитивов 1…10 множеством поверхностей A…F. Эта задача относится к задачам классификации объектов, которая формулируется так: требуется выполнить разбиение исходного множества Мчерт на подмножества (классы) ωi, каждый из которых определяет поверхность πi, ограничивающую рассматриваемую деталь D, так чтобы выполнялись соотношения
При построении модели используются п– арные отношения, связанные с образованием поверхностей π1 … π10. К унарным отношениям (R(1)) относятся на множестве М модели М относятся тип поверхности, ее размеры, ориентация в пространстве. К п- арным отношениям R(n) относятся характеристики относительного расположения поверхностей, такие как отношения перпендикулярности, параллельности, соосности и др. Очевидно, п- арность отношения связана с типом образующей поверхности и правилами вывода отношения R(n).
Рассмотрим 
основные правила, лежащие в основе образования п- арных отношений модели М.
Правило образования отношения R(1) (торец А) можно сформулировать так: два примитива 
и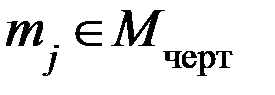 
образуют один класс (торец), если выполняются соотношения
Эти правила следует понимать так: существует осевая линия mj (свойство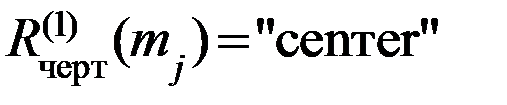 
) и отрезок сплошной прямой линии mi (
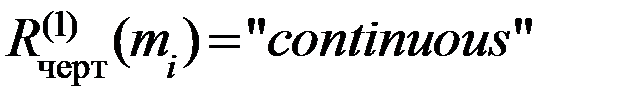), перпендикулярный mj (условие 4) и симметричный mj (условие 1…3).
Приведенное правило позволяет объединить примитивы (1,10) а также (5, 10) в один класс – торец.
Если кольцевой торец образован двумя отрезками прямых, то правило образования класса «торец» усложняется:
В этом случае добавляется условие параллельности двух отрезков (cb) и (mn) (пункт 5).
Правило образования отношения R(n) (цилиндрическая поверхность n) можно сформулировать так: три примитива mi є Mчерт образуют один класс (цилиндрическая поверхность), если выполняются соотношения:
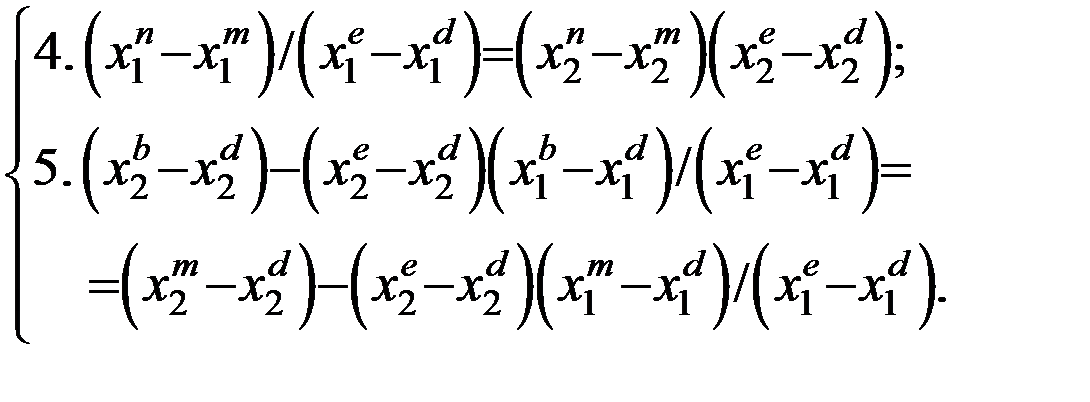
Это правило следует понимать так: существует осевая линия mj (свойство 
) такая, что отрезки сплошных прямых линий mi и mk параллельны mj (условия 3,4) и симметричны относительно осевой линии mj (условие 5).
В таблице 8.1 показано содержание каждого множества из одномерных примитивов.
Таблица 8.1
Поиск по сайту: