 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Проверка оптимальности
После того как все потенциалы найдены, следует для всех свободных клеток вычислить разности 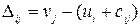 :
:
Δ21 = 4 – (-1 + 1) = 4, Δ31 = 4 – (0 + 5) = -1,
Δ32 = 2 – (0 + 4) = -2, Δ13 = 2 – (0 + 5) = -3,
Δ14 = 0 – (0 + 0) = 0, Δ24 = 0 – (0 + -1) = 1.
Среди вычисленных разностей имеются положительные. Значит, опорный план, построенный выше, не является оптимальным.
Замечание. По своему экономическому смыслу величина  характеризует изменение в общих затратах на перевозки, которое произойдет, если будет осуществлена перевозка единицы груза от поставщика i потребителю j. Поэтому, если
характеризует изменение в общих затратах на перевозки, которое произойдет, если будет осуществлена перевозка единицы груза от поставщика i потребителю j. Поэтому, если  > 0, то это означает, что существует свободное направление перевозки груза, экономящее затраты, т.е. текущий план перевозок не оптимален. Если же все
> 0, то это означает, что существует свободное направление перевозки груза, экономящее затраты, т.е. текущий план перевозок не оптимален. Если же все  , то это означает, что нет свободных направлений перевозок, экономящих затраты, т.е. текущий план перевозок оптимален.
, то это означает, что нет свободных направлений перевозок, экономящих затраты, т.е. текущий план перевозок оптимален.
Следующим этапом является построение нового опорного плана с меньшим значением целевой функции.
2.3. Построение нового опорного плана
Для построения «лучшего» опорного плана нужно найти свободную клетку, которой соответствует наибольшая положительная разность  . Если таких клеток несколько, то берется любая из них.
. Если таких клеток несколько, то берется любая из них.
Затем строится новый план перевозок, в котором эта клетка будет занятой, т.е. будет осуществлена перевозка из пункта i в пункт j. Так как число занятых клеток меняться не должно, то одна из ранее занятых клеток освобождается. Освобождаемая клетка и новые объемы перевозок в занятых клетках определяются с помощью цикла.
Циклом называется набор клеток таблицы, которые можно соединить замкнутой ломаной линией, которая в каждой клетке совершает поворот на 90° и удовлетворяет таким условиям:
1. любое звено ломаной находится либо в строке, либо в столбце таблицы;
2. никакие два ее звена не могут находиться в одной строке или в одном столбце.
Одной из вершин цикла должна быть выбранная свободная клетка, а его остальные вершины должны находиться в занятых клетках. При построении любого цикла нужно следовать следующему правилу: выйдя из клетки в горизонтальном (вертикальном) направлении нужно остановиться на такой клетке, из которой затем можно двигаться по вертикали (горизонтали). Для этого в соответствующем столбце (строке) должно быть более одной занятой клетки. В построенном цикле, начиная с выбранной клетки, помечаются вершины: нечетные — знаком "+", а четные — знаком "–".
Знаком "+" помечаются те клетки, в которых объемы перевозок должны увеличиться. Знаком "–" помечаются клетки, в которых объемы перевозок должны уменьшиться, чтобы сохранился баланс перевозок. Среди клеток, помеченных знаком "–", определяется клетка, которой соответствует наименьшая величина перевозки xij. Обозначим эту величину символом θ.
Значения перевозок в остальных помеченных клетках пересчитываются по такому правилу: к объемам перевозок, содержащихся в «плюсовых» клетках, добавляется величина перевозки θ, а из объемов перевозок, содержащихся в «минусовых» клетках, вычитается величина перевозки θ. Остальные занятые клетки не изменяются. Если в результате этой операции только одна из «минусовых» клеток содержит нулевое значение, то она освобождается. Если же таких клеток несколько, то освобождается та из них, которая имеет максимальный тариф перевозок, а остальные остаются занятыми и содержат нули. В этом случае новый опорный план будет вырожденным.
На этом процедура построения нового опорного плана завершается, и он проверяется на оптимальность, т.е. происходит возврат к первому этапу. Значение целевой функции на новом плане уменьшается по сравнению со старым значением на величину, равную θ·  .
.
Построим новый опорный план, улучшающий начальный опорный план. Ранее мы нашли разности  для всех свободных клеток. Максимальная разность, равная 4, находится в клетке (2, 1). Следовательно, эту клетку нужно загрузить.
для всех свободных клеток. Максимальная разность, равная 4, находится в клетке (2, 1). Следовательно, эту клетку нужно загрузить.
Таблица 4
| 4 – | 2 + | u 1 = 0 | |||
 25 25
| |||||
| 1 + | 3 – | u 2 = -1 | |||
| u 3 = 0 | |||||
| v 1 = 4 | v 2 = 2 | v 3 = 2 | v 4 = 0 | Z = 260 |
Строим цикл, который позволит определить освобождаемую клетку. В данном случае он находится легко: его вершины образуют клетки: (2, 1), (1, 1), (1, 2) и (2, 2). Пометим знаком "+" клетки (2, 1) и (1, 2): в них объемы перевозок должны увеличиться. Клетки (1, 1) и (2, 2) пометим знаком "–": в них объемы перевозок уменьшаются.
Определим величину перевозки θ в клетке (2,1), которая загружается. Она равна минимальному значению из содержащихся в «минусовых» клетках (1, 1) и (2, 2), т.е. θ = min {25, 5} = 5. Это значение содержится в клетке (2, 2); следовательно, она освобождается. Новые значения в клетках, являющихся вершинами цикла, таковы:
 ,
,
 ,
,
 .
.
Затраты на перевозки в новом плане равны 240. Они уменьшились по сравнению с затратами на перевозки в старом плане на Δ21·θ =4·5 = 20.
Проверим, является ли найденный опорный план оптимальным. Для этого снова вычислим потенциалы. Снова положим u 1 = 0. Затем с учетом сделанного замечания, найдем значения остальных потенциалов: v 1 = 4, v 2 = 2, u 2 = 3, v 3 = 6, u 3 = 4, v 4 = 4 и занесем найденные значения в таблицу. Для всех свободных клеток вычислим разности  :
:
Δ22 = 2 – (3 + 3) = -4, Δ31 = 4 – (5 + 4) = -5,
Δ32 = 2 – (4 + 4) = -6, Δ13 = 6 – (0 + 5) = 1,
Δ24 = 4 – (0 + 3) = 1, Δ14 = 4 – (0 + 0) = 4.
Снова имеются положительные разности. Значит, построенный план не является оптимальным. Максимальную разность, равную 4, дает клетка (1, 4), следовательно ее нужно взять в качестве загружаемой.
Построим цикл с вершиной в этой клетке. На этот раз ситуация существенно сложнее, чем в предыдущем случае. Следуя описанному выше правилу построения цикла, мы должны, выйдя из клетки (1, 4) переместиться в клетку (3, 4); далее — в клетки (3, 3), (2, 3), (2, 1), (1, 1) и вернуться в начальную клетку (см. табл. 5).
Таблица 5
 4 – 4 –
| 0 + | u 1 = 0 | |||
| 1 + | 3 – | u 2 = 3 | |||
| 2 + | 0 – | u 3 = 4 | |||
| v 1 = 4 | v 2 = 2 | v 3 = 6 | v 4 = 4 | Z = 240 |
Итак, вершинами цикла будут клетки (1, 4), (3, 4), (3, 3), (2, 3), (2, 1) и (1, 1). В этом цикле «минусовыми» являются клетки (1, 1), (2, 3) и (3, 4). Найдем минимальное значение в этих клетках: θ = min{20, 25, 40} = 20. Оно содержится в клетке (1, 1). Следовательно, она освобождается. Новые значения в остальных клетках, являющихся вершинами цикла, таковы:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Новое значение целевой функции равно 160. Оно уменьшилось по сравнению с затратами на перевозки в старом плане на Δ14·θ = 20·4 = 80. Проверим построенный план на оптимальность.
Таблица 6
| u 1 = 0 | |||||
 3 – 3 –
| 0 + | u 2 = -1 | |||
| 2 + | 0 – | u 3 = 0 | |||
| v 1 = 0 | v 2 = 2 | v 3 = 2 | v 4 =0 | Z = 160 |
Для этого вычислим потенциалы. Положим u 1 = 0. Затем найдем значения остальных потенциалов: v 2 = 2, v 4 = 0, u 3 = 0, v 3 = 2, u 2 = -1, v 1 = 0 и занесем найденные значения в таблицу 6. Для всех свободных клеток вычислим разности  :
:
Δ11 = 0 – (4 + 0) = -4, Δ13 = 2 – (5 + 0) = -3,
Δ22 = 2 – (3 – 1) = 0, Δ24 = 0 – (0 – 1) = 1,
Δ31 = 0 – (0 + 5) = -5, Δ32 = 2 – (0 + 4) = -2.
Снова имеется клетка (2, 4) с положительной разностью. Значит, построенный план не является оптимальным и эту клетку нужно взять в качестве загружаемой.
Таблица 7
| u 1 = 0 | |||||
| u 2 = 0 | |||||
| u 3 = 0 | |||||
| v 1 = 1 | v 2 = 2 | v 3 = 2 | v 4 =0 | Z = 155 |
Строим цикл, который позволит определить освобождаемую клетку. Его вершины образуют клетки: (2, 4), (3, 4), (3, 3) и (2, 3). Пометим знаком "+" клетки (2, 4) и (3, 3): в них объемы перевозок должны увеличиться. Клетки (2, 3) и (3, 4) пометим знаком "–": в них объемы перевозок уменьшаются.
Определим величину перевозки θ в клетке (2,4), которая загружается. Она равна минимальному значению из содержащихся в «минусовых» клетках (2, 3) и (3, 4), т.е. θ = min {5, 20} = 5. Это значение содержится в клетке (2, 3); следовательно, она освобождается. Новые значения в клетках, являющихся вершинами цикла, таковы:
 ,
,
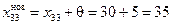 ,
,
 .
.
Затраты на перевозки в новом плане равны 155. Они уменьшились по сравнению с затратами на перевозки в старом плане на Δ24·θ =1·5 = 5.
Проверим построенный план на оптимальность. Для этого вычислим потенциалы. Положим u 1 = 0. Затем найдем значения остальных потенциалов: v 2 = 2, v 4 = 0, u 3 = 0, v 3 = 2, u 2 = 0, v 1 = 1 и занесем найденные значения в таблицу. Для всех свободных клеток вычислим разности  :
:
Δ11 = 1 – (4 + 0) = -3, Δ13 = 2 – (5 + 0) = -3,
Δ22 = 2 – (3 + 0) = -1, Δ23 = 2 – (3 + 0) = -1,
Δ31 = 1 – (0 + 5) = -4, Δ32 = 2 – (0 + 4) = -2.
Все разности неположительные. Значит, найденный план перевозок оптимален (см. табл. 7).
Ответ:
| – | – | ||||
| Х* = | – | – | Z* = 155 | ||
| – | – |
Экономическая интерпретация полученных результатов:
Осуществляются такие перевозки:
· первый магазин получает со второго склада 25 единиц;
· второй магазин получает с первого склада 30 единиц;
· третий магазин получает с третьего склада 35 единиц.
Поставки в фиктивный четвертый магазин означают, что на первом складе осталось 20 единиц, на втором складе – 5 единиц, а на третьем складе – 15 единиц груза.
Общие затраты на перевозки в оптимальном плане равны 155.
Поиск по сайту: