АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

V2: ДЕ 6 - Линейные отображения. Определители второго порядка

Читайте также:
  1. A) линейные
  2. II ОБЩИЕ НАЧАЛА ПУБЛИЧНО-ПРАВОВОГО ПОРЯДКА
  3. II. САКРАЛЬНАЯ ГЕОМЕТРИЯ: МЕТАФОРА УНИВЕРСАЛЬНОГО ПОРЯДКА
  4. IV.1. Общие начала частной правозащиты и судебного порядка
  5. V2: ДЕ 11 - Векторные пространства. Линейные операции над векторами
  6. V2: ДЕ 4 – Линейные отображения. Линейные операции над матрицами
  7. V2: ДЕ 5 - Линейные отображения. Умножение матриц
  8. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
  9. V2: ДЕ 54 - Дифференциальные уравнения, допускающие понижение порядка
  10. Абстрактные линейные системы
  11. Адаптивная полиномиальная модель первого порядка

I: {{6.1}}

S: Определитель равен нулю при α равном ###

+: 3

 

I: {{6.2}}

S: Определитель 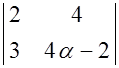равен нулю при α равном ###

+: 2

 

I: {{6.3}}

S: Определитель равен нулю при α равном ###

+: 2

 

I: {{6.4}}

S: Определитель равен нулю при α равном ###

+: 1

 

I: {{6.5}}

S: Определитель матрицы равен нулю при α равном ###

+: 3

 

I: {{6.6}}

S: Определитель матрицы равен нулю при α равном ###

+: 2

 

I: {{6.7}}

S: Определитель матрицы равен нулю при α равном ###

+:-1

 

I: {{6.8}}

S: Определитель равен нулю при α равном ###

+: 3

 

I: {{6.9}}

S: Определитель равен нулю при α равном ###

+: -1

 

I: {{6.10}}

S: Определитель равен нулю при α равном ###

+: 6

 

I: {{6.11}}

S: Определитель равен нулю при α равном ###

+: 11

 

I: {{6.12}}

S: Определитель равен нулю при α равном ###

+: -1

 

I: {{6.13}}

S: Определитель 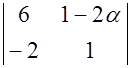равен нулю при α равном ###

+: 2

 

I: {{6.14}}

S: Определитель равен нулю при α равном ###

+: 3

 

I: {{6.15}}

S: Определитель матрицы 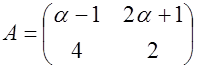равен нулю при α равном ###

+: -1

 

I: {{6.16}}

S: Определитель матрицы 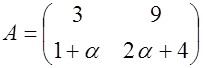равен нулю при α равном ###

+: 1

 

I: {{6.17}}

S: Определитель матрицы равен нулю при α равном ###

+: 2

 

I: {{6.18}}

S: Определитель 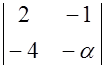равен нулю при α равном ###

+: -2

 

I: {{6.19}}

S: Определитель равен нулю при α равном ###

+: 2

 

I: {{6.20}}

S: Определитель равен нулю при α равном ###

+: -1

 

I: {{6.21}}

S: Определитель равен нулю при α равном ###

+: -2

 

I: {{6.22}}

S: Определитель 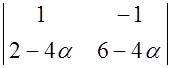равен нулю при α равном ###

+: 1

 

I: {{6.23}}

S: Определитель равен нулю при α равном ###

+: 1

 

I: {{6.24}}

S: Определитель равен нулю при α равном ###

+: -1

 

I: {{6.25}}

S: Определитель матрицы равен нулю при α равном ###

+: 2


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)