 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Коды Хэмминга — вероятно, наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления
Построение кодов Хемминга основано на принципе проверки на четность числа единичных символов: к последовательности добавляется такой элемент, чтобы число единичных символов в получившейся последовательности было четным.  знак
знак  здесь означает сложение по модулю 2
здесь означает сложение по модулю 2
 .
.  - ошибки нет,
- ошибки нет,  однократная ошибка. Такой код называется
однократная ошибка. Такой код называется  или
или  . Первое число - количество элементов последовательности, второе - количество информационных символов. Для каждого числа проверочных символов
. Первое число - количество элементов последовательности, второе - количество информационных символов. Для каждого числа проверочных символов 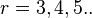 существует классический код Хемминга с маркировкой
существует классический код Хемминга с маркировкой  т.е. -
т.е. -  . При иных значениях k получается так называемый усеченный код, например международный телеграфный код МТК-2, у которого
. При иных значениях k получается так называемый усеченный код, например международный телеграфный код МТК-2, у которого  . Для него необходим код Хемминга
. Для него необходим код Хемминга  , который является усеченным от классического
, который является усеченным от классического  . Для Примера рассмотрим классический код Хемминга
. Для Примера рассмотрим классический код Хемминга  . Сгруппируем проверочные символы следующим образом:
. Сгруппируем проверочные символы следующим образом:



знак  здесь означает сложение по модулю 2.
здесь означает сложение по модулю 2.
Получение кодового слова выглядит следующим образом:
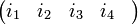
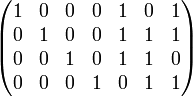 =
= 
На вход декодера поступает кодовое слово  где штрихом помечены символы, которые могут исказиться в результате помехи. В декодере в режиме исправления ошибок строится последовательность синдромов:
где штрихом помечены символы, которые могут исказиться в результате помехи. В декодере в режиме исправления ошибок строится последовательность синдромов:



 называется синдромом последовательности.
называется синдромом последовательности.
Систематические коды[править | править вики-текст]
Систематические коды образуют большую группу из блочных, разделимых кодов (в которых все символы можно разделить на проверочные и информационные). Особенностью систематических кодов является то, что проверочные символы образуются в результате линейных операций над информационными символами. Кроме того, любая разрешенная кодовая комбинация может быть получена в результате линейных операций над набором линейно независимых кодовых комбинаций.
Самоконтролирующиеся коды[править | править вики-текст]
Коды Хэмминга являются самоконтролирующимися кодами, то есть кодами, позволяющими автоматически обнаруживать ошибки при передаче данных. Для их построения достаточно приписать к каждому слову один добавочный (контрольный) двоичный разряд и выбрать цифру этого разряда так, чтобы общее количество единиц в изображении любого числа было, например, нечетным. Одиночная ошибка в каком-либо разряде передаваемого слова (в том числе, может быть, и в контрольном разряде) изменит четность общего количества единиц. Счетчики по модулю 2, подсчитывающие количество единиц, которые содержатся среди двоичных цифр числа, могут давать сигнал о наличии ошибок.
При этом невозможно узнать, в каком именно разряде произошла ошибка, и, следовательно, нет возможности исправить её. Остаются незамеченными также ошибки, возникающие одновременно в двух, четырёх, и т.д. — в четном количестве разрядов. Впрочем, двойные, а тем более четырёхкратные ошибки полагаются маловероятными.
Самокорректирующиеся коды[править | править вики-текст]
Коды, в которых возможно автоматическое исправление ошибок, называются самокорректирующимися. Для построения самокорректирующегося кода, рассчитанного на исправление одиночных ошибок, одного контрольного разряда недостаточно. Как видно из дальнейшего, количество контрольных разрядов k должно быть выбрано так, чтобы удовлетворялось неравенство  или
или  , где m — количество основных двоичных разрядов кодового слова. Минимальные значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице.
, где m — количество основных двоичных разрядов кодового слова. Минимальные значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице.
| Диапазон m | kmin |
| 2-4 | |
| 5-11 | |
| 12-26 | |
| 27-57 |
В настоящее время наибольший интерес представляют двоичные блочные корректирующие коды. При использовании таких кодов информация передаётся в виде блоков одинаковой длины и каждый блок кодируется и декодируется независимо друг от друга. Почти во всех блочных кодах символы можно разделить на информационные и проверочные. Таким образом, все комбинации кодов разделяются на разрешенные (для которых соотношение информационных и проверочных символов возможно) и запрещенные.
Основными характеристиками самокорректирующихся кодов являются:
1. Число разрешенных и запрещенных комбинаций. Если n - число символов в блоке, r - число проверочных символов в блоке, k - число информационных символов, то  - число возможных кодовых комбинаций,
- число возможных кодовых комбинаций,  - число разрешенных кодовых комбинаций,
- число разрешенных кодовых комбинаций,  - число запрещенных комбинаций.
- число запрещенных комбинаций.
2. Избыточность кода. Величину  называют избыточностью корректирующего кода.
называют избыточностью корректирующего кода.
Поиск по сайту: