АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

ПОЛЮСЫ И НУЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ

Читайте также:
  1. II. Основные задачи и функции
  2. III. Предмет, метод и функции философии.
  3. IV. Конструкция бент-функции
  4. Ms Excel: мастер функций. Логические функции.
  5. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  6. V2: ДЕ 32 - Дифференциальное исчисление функции одной переменной. Производная
  7. V2: ДЕ 35 - Дифференциальное исчисление функции одной переменной. Производные высший порядков
  8. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  9. V2: Функции исторической науки
  10. VIII. ФУНКЦИИ НАУЧНОГО ИССЛЕДОВАНИЯ
  11. XVIII. ПРОЦЕДУРЫ И ФУНКЦИИ
  12. А) ПЕРЕДАЧА НА РУССКОМ ЯЗЫКЕ ФУНКЦИИ АРТИКЛЯ

При анализе дискретных фильтров имеет значение определение положения полюсов и нулей передаточной функции в z-плоскости.

• Полюс — это корень полинома в знаменателе, а нуль — корень полинома в числителе передаточной функции.

• Если полином имеет вещественные коэффициенты, то его корни могут быть вещественными и/или комплексно-сопряженными.

• При определении значений нулей и полюсов в z-плоскости целесообразно преобразовать передаточную функцию к виду без отрицательных степеней z.

• Полином второй степени имеет либо 2 вещественных корня

либо 2 комплексно-сопряженных корня

где

Действительно, если разложить полином на простые множители

Рис. 2 Карты нулей и полюсов базового РФ 1-го порядка

Базовый рекурсивный фильтр 1-so порядка. Преобразуем к виду, без отрицательных степеней z . Передаточная функция имеет один нуль в точке 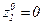и один полюс в точке . На рис. 2 изображены карты нулей и полюсов фильтра в z-плоскость при и .

• Рекурсивный фильтр 1-го порядка. Для определения нулей и полюсов преобразуем передаточную функцию рекурсивного фильтра 1-го порядка к виду, без отрицательных степеней z .

Рис. 3 Карта нулей и полюсов РФ 1-го порядка

Передаточная функция H(z) имеет один нуль в точке и один полюс в точке .

На рис. 3 изображена карта нулей и полюсов фильтра при bo = 0.2, b1 = - 0.2, а1 = 0.8.

• Базовый рекурсивный фильтр 2-го порядка. Рассмотрим случай комплексно-сопряженных полюсов. Передаточная функция

Рис. 4. Карта нулей и полюсов базового РФ 2-го порядка

имеет два нуля в точке и два полюса , где , .

На рис. 4 изображена карта нулей и полюсов фильтра в z-плоскости при a1= -0.8, a2 = 0.64.При этом , .

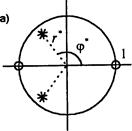Рис. 5 Карты нулей и полюсов РФ 2-го порядка

• Рекурсивный фильтр 2-гo порядка. Рассмотрим случай комплексно-сопряженных полюсов. Передаточная функция имеет два полюса , где , и два нуля . В случае вещественных нулей

в случае комплексно-сопряженных нулей , где , .

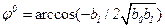На рис. 5 изображена карта нулей и полюсов фильтра в z-плоскости для двух случаев.

• bo = 0.2, bi = 0, Ъг = -0.2, a1 = 0.9, a2 = 0.81 [вещественные нули).

В этом случае .

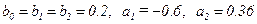• (комплексно-сопряженные нули).

В этом случае

 


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)