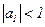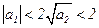Устойчивость дискретных фильтров

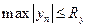Дискретный фильтр называется устойчивым, если при произвольных начальных условиях реакция на любое ограниченное воздействие также ограничена, т.е. если , то , где

Критерием устойчивости дискретного фильтра является абсолютная сходимость ряда отсчетов импульсной характеристики:

Действительно, если представить в виде (1.30)

Рис. 6 Пояснение критерия устойчивости

,

то

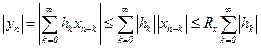
откуда следует (1.55).

• Существует другой, более простой для применения, критерий устойчивости дискретного фильтра: все полюса передаточной функции должны находиться внутри единичного круга z-плоскости (рис. 6), т. е.

Действительно, так как , то можно получить

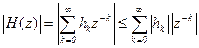
Допустим, что 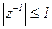, т.e. 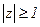. Тогда и из выражения получим

Для устойчивого фильтра должно выполняться условие, т. е.

.

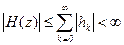Следовательно, Н(z) должна быть конечна во всех точках z -плоскости, где | z | > 1. Очевидно, что в полюсе (при ) H(z)=w. Отсюда следует, что передаточная функция не должна иметь полюсов на единичной окружности и вне ее, т. е. должно выполняться условие.

Отметим, что:

• КИХ-фильтр всегда устойчив, так как его импульсная характеристика имеет конечную длину (см.).

• Рекурсивный фильтр устойчив, если устойчивым является соответствующей ему базовый фильтр. Это объясняется тем, что нули передаточной функции (т. е. вид полинома в числителе) не влияют на устойчивость фильтра.

Таблица 1. Ограничения на коэффициенты РФ Фильтр Коэффициент а1 Коэ Ф >фж циёит Д|   Коэффициент а2   1-го порядка нет 2-го порядка

Условие накладывает определенные ограничения на величину коэффициентов знаменателя передаточной функции рекурсивного фильтра. Для РФ 1-го порядка и РФ 2-го порядка с комплексно-сопряженными полюсами эти ограничения приведены в табл. 1.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется передаточной функцией?

2. Как связано разностное уравнение дискретного фильтра с его передаточной функцией?

3. Запишите формулы для передаточных функций основных типов фильтров.

4. Охарактеризуйте импульсную характеристику ДФ.

5. Как связана передаточная функция дискретного фильтра с его частотной характеристикой?

6. Дайте понятие устойчивости ДФ.

7. Приведите критерии устойчивости ДФ.

8. Какое положение на комплексной z-плоскости занимают полюсы устойчивых (неустойчивых) ДФ?

9. Какие ограничения накладывает требование устойчивости на коэффициенты передаточной функции фильтра 1-го и 2-гопорядков.

10. Как переходят от ненормированной частоты к нормированной и обратно?

Литература

1. Куприянов М.С., Матюшкин Б.Д. Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. - 2-е изд., перераб. и доп. - СПб.: Политтехника, 1999. - 592 с.: ил.

2. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. - М.: Мир, 1978.

3. Mathcad 6.0 plus. Финансовые, инженерные и научные расчеты в среде Windows 95. Издание 2-е, стереотипное- М.:"Филинъ", 1977.

Поиск по сайту: