 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Влияние формы дискретизирующих импульсов
Запишем выражение (3.3) в более общей форме, используя вместо дельта-функций импульсы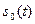 
произвольной формы:
(3.9)
Получить выражение для спектральной функции сигнала (3.9) будет проще всего, если рассмотреть этот сигнал как результат прохождения последовательности дельта-функций (3.3) через линейную стационарную систему с импульсной характеристикой 
(t). Действительно, при этом каждая из дельта-функций в (3.3) будет порождать на выходе цепи сигнал (t) с соответствующими временной задержкой и амплитудным множителем, так что в результате получится именно выражение (3.9).
Поскольку при прохождении сигнала через линейную систему с постоянными параметрами его спектр умножается на комплексный коэффициент передачи этой системы (см. главу 2), спектр сигнала (3.9) будет отличаться от выражения (3.7) лишь дополнительным множителем — спектром импульса (t):
Итак, отличие формы дискретизирующих импульсов от дельта-функций вызывает мультипликативные искажения спектра дискретного сигнала. Спектральная функция импульса, имеющего конечную энергию, затухает с ростом частоты, поэтому возникающие при дискретизации сдвинутые копии спектра сигнала s(t) оказываются ослабленными.
Рассмотрим важный с практической точки зрения случай, когда s0(t) представляет собой прямоугольный импульс с единичной амплитудой и длительностью, равной периоду дискретизации (рис. 3.9, слева). В данном случае дискретный сигнал приобретает ступенчатую форму, что характерно для сигнала на выходе ЦАП перед сглаживающим фильтром (см. рис. 3.2). Искажения спектра при этом описываются множителем 
следующего вида:
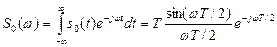
График модуля функции приведен на рис. 3.9 справа. Спад амплитудного спектра на частоте Найквиста, равной 
/Т, составляет
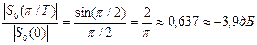
В качестве примера на рис. 3.10 приведены результаты дискретизации треугольного импульса дельта-функциями и рассмотренными прямоугольными импульсами.
Из графиков видно, что ЦАП сам по себе является фильтром нижних частот, однако с весьма невысокой степенью подавления сдвинутых копий спектра. Кроме того, поскольку АЧХ такого фильтра весьма далека от прямоугольной, он обладает сильной неравномерностью в полосе пропускания и заметно ослабляет высокочастотные составляющие сигнала (на частоте Найквиста ослабление составляет почти 4 дБ).
Поиск по сайту: